曲率半径公式推导
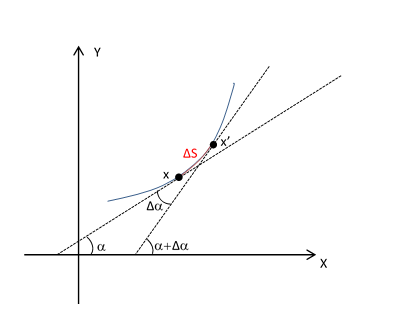
曲率(k):描述曲线下降长度随角度变化,${ m{k}} = mathop {lim }limits_{alpha o 0} left| {frac{{Delta alpha }}{{Delta s}}} ight|$
$R = frac{1}{k} = frac{{{{left[ {1 + {{left( {frac{{dy}}{{dx}}} ight)}^2}} ight]}^{frac{3}{2}}}}}{{frac{{{d^2}y}}{{d{x^2}}}}} = frac{{{{left[ {1 + {{left( {f'} ight)}^2}} ight]}^{frac{3}{2}}}}}{{f''}}$ (1)
曲率半径计算公式
推导过程
- 曲线上某点的曲率半径是该点的密切圆的半径,在$mathop {lim }limits_{Delta { m{s}} o 0} frac{{Delta alpha }}{{Delta s}} = frac{{dalpha }}{{ds}}$存在的条件下,${ m{k}} = left| {frac{{dalpha }}{{ds}}} ight|$。
- 设曲线的方程为y=f(x),且f(x)具有二阶导数。因为tanα = y’(设-$pi $/2<α<$pi $/2),所以
a=arctany’
$frac{{{ m{d}}alpha }}{{dx}} = {left( {{ m{arctany'}}} ight)^prime }$
[dalpha = {left( {arctan y'} ight)^prime }dx = frac{{y''}}{{1 + {{y'}^2}}}dx]
或者
sec2αdα=y''dx,
${ m{d}}alpha = frac{{y''}}{{se{c^2}alpha }}dx = frac{{y''}}{{1 + ta{n^2}alpha }}dx = frac{{y''}}{{1 + {y^{'2}}}}dx$
3. 因为 ${ m{ds}} = sqrt {1 + {y^{'2}}} { m{dx}}$(密切圆面积求导),从而得到曲率公式${ m{k}} = frac{{f''}}{{{{left[ {1 + {{left( {f'} ight)}^2}} ight]}^{frac{3}{2}}}}}$。
参考链接:https://jingyan.baidu.com/album/7f41ecec213a10593d095c26.html?picindex=4
【 结束 】