题目链接:http://poj.org/problem?id=1177
题目大意:若干个矩形,求这些矩形重叠形成的图形的轮廓周长。
解题思路:这里引用一下大牛的思路:kuangbin
总体思路:
1.沿X轴离散化建树
2.按Y值从小到大排序平行与X轴的边,然后顺序处理
如果遇到矩形下面那条边则插入到线段树中,遇到矩形上面的边则将相应的边删除掉
根据线段树当前的状态统计长度
第二点是本题的核心思想,偶再举个例:
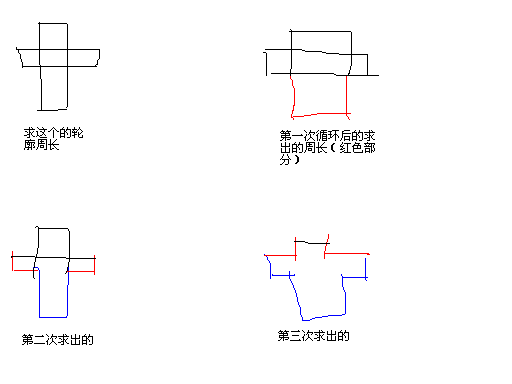
第一次求出的部分很好理解.
第二次求出的为什么会少了中间那部分.那是因为插入的新线段覆盖了第一条,此时线段树返回的长度是新的那一条的长度,将这个值再减去上次的就少了中间那部分
第三次因为是矩形的上边,所以要删除在那条长的线段.此时的线段树返回的则是第一次的长度,将此值减去第二次返回值,再取其负值就是红色X轴那部分了
最后那条X轴的,再补上就行了。
我写的稍微有点不同,不过大概也就是这个思路了。总结一下就是矩形下位边cnt+1,上位边cnt-1,求tree[1].sum,这些步骤跟求矩形面积并是一样的。
然后按照扫描线从小到大一次跟新,ans+=abs(上一次的测度-更新后的测度)。
然后就按x,y方向扫描线各求一遍,加在一起就是总的周长。(好像还是有点问题,就是重边会出错,不会改啊!!!算了,等以后变强了再来改0 0)
这题我没有离散化,因为数据不是很大也没有小数所以就懒得写了。。。
代码:
1 #include<cstdio> 2 #include<cmath> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<vector> 7 #include<queue> 8 #include<set> 9 #include<map> 10 #include<stack> 11 #include<string> 12 #define LC(a) (a<<1) 13 #define RC(a) (a<<1|1) 14 #define MID(a,b) ((a+b)>>1) 15 using namespace std; 16 typedef long long LL; 17 const int INF=0x3f3f3f3f; 18 const int N=1e4+5; 19 20 struct Node{ 21 int l,r,cnt,sum;//sum为测度 22 }tree[N*2*4]; 23 24 struct node{ 25 int l,r,h,flag; 26 node(){} 27 node(double a,double b,double c,double d){ 28 l=a;r=b;h=c;flag=d; 29 } 30 }a[N],b[N]; 31 32 bool cmp(node a,node b){ 33 return a.h<b.h; 34 } 35 //因为每条线段对应删除的线段是严格出现的,不需要Lazy也就不需要pushdown() 36 void pushup(int p) { 37 if(tree[p].cnt>0) 38 tree[p].sum=tree[p].r-tree[p].l+1; 39 else if(tree[p].l==tree[p].r) 40 tree[p].sum=0; 41 else 42 tree[p].sum=tree[LC(p)].sum+tree[RC(p)].sum; 43 } 44 45 void build(int p,int l,int r){ 46 tree[p].l=l; 47 tree[p].r=r; 48 if(l==r){ 49 tree[p].cnt=tree[p].sum=0; 50 return; 51 } 52 build(LC(p),l,MID(l,r)); 53 build(RC(p),MID(l,r)+1,r); 54 pushup(p); 55 } 56 57 void update(int p,int l,int r,int cnt){ 58 if(l>tree[p].r||r<tree[p].l) 59 return; 60 if(l<=tree[p].l&&r>=tree[p].r&&tree[p].cnt!=-1){ 61 tree[p].cnt+=cnt; 62 pushup(p); 63 return; 64 } 65 update(LC(p),l,r,cnt); 66 update(RC(p),l,r,cnt); 67 pushup(p); 68 } 69 70 int main(){ 71 int n; 72 while(~scanf("%d",&n)){ 73 int m1=0,m2=1; 74 for(int i=1;i<=n;i++){ 75 int x1,x2,y1,y2; 76 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 77 x1+=N,x2+=N,y1+=N,y2+=N;//防止x,y出现负数 78 a[++m1]=node(x1,x2,y1,1); 79 b[m1]=node(y1,y2,x1,1); 80 a[++m1]=node(x1,x2,y2,-1); 81 b[m1]=node(y1,y2,x2,-1); 82 } 83 sort(a+1,a+1+m1,cmp); 84 sort(b+1,b+1+m1,cmp); 85 //自下往上扫描一遍 86 build(1,1,2*N-1); 87 int ans=0; 88 for(int i=1;i<=m1;i++){ 89 int last=tree[1].sum; 90 int l=a[i].l; 91 int r=a[i].r-1; 92 update(1,l,r,a[i].flag); 93 ans+=abs(tree[1].sum-last); 94 } 95 //自左往右扫描一遍 96 build(1,1,2*N-1); 97 for(int i=1;i<=m1;i++){ 98 int last=tree[1].sum; 99 int l=b[i].l; 100 int r=b[i].r-1; 101 update(1,l,r,b[i].flag); 102 ans+=abs(tree[1].sum-last); 103 } 104 printf("%d ",ans); 105 } 106 return 0; 107 }