一、题目描述
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
示例 1:
输入: 2
输出: [0,1,1]
示例 2:
输入: 5
输出: [0,1,1,2,1,2]
要求:
①给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗?
②要求算法的空间复杂度为O(n)。
二、思路分析
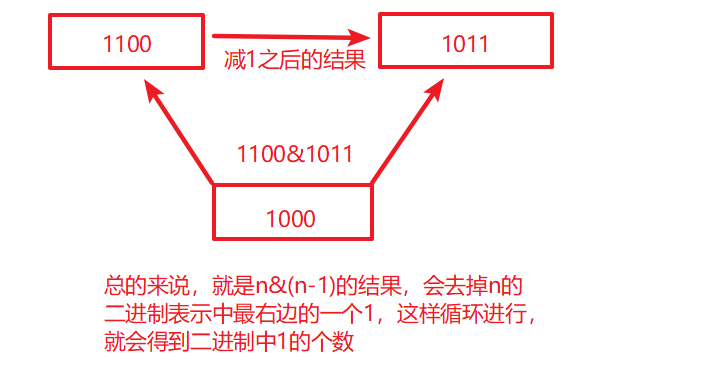
1、我们首先来看一下单个int整数的二进制中1的个数的计算方法
2、按照上面这种方式,可以得到下面的代码,实现求一个int类型的二进制表示中1的个数
1 /** 2 * 计算单个int的二进制1的个数 3 * @param n 4 * @return 5 */ 6 public static int NumberOf1(int n) { 7 int countOfOne = 0; 8 while(n != 0) { 9 countOfOne ++; 10 n = n & (n - 1); 11 } 12 return countOfOne; 13 }
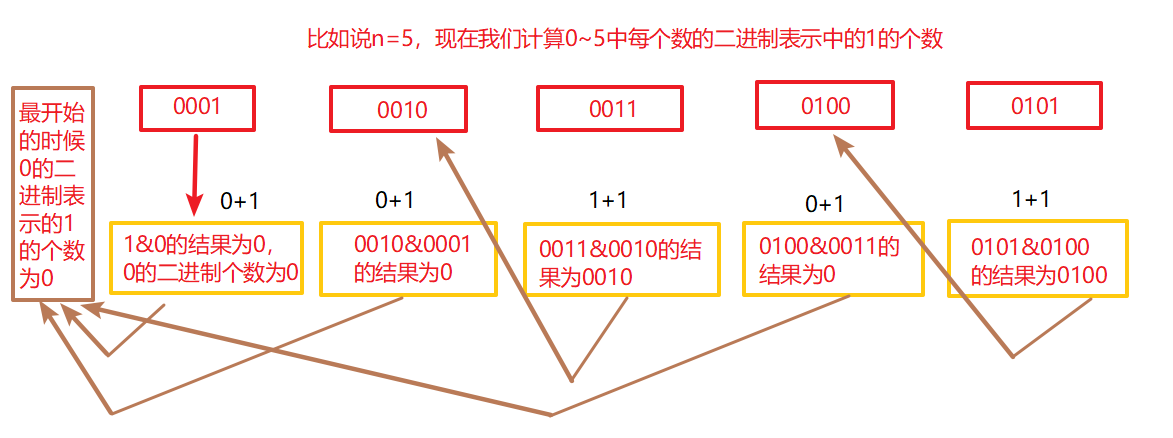
3、下面,我们来思考上面的题目:既然n&(n-1)可以去掉n的二进制表示中最右边的那个1,那么我们计算n的二进制中1的个数之前,n&(n-1)这个数,可以说恰好就是比n小的上一次计算(二进制中1)的个数,我们可以借助额外空间存储上次计算过的值,然后再加1就是n的二进制表示中的1的个数。可以参考下面这个图
三、代码实现
1 package cn.zifuchuan; 2 3 public class Test6 { 4 5 public static void main(String[] args) { 6 int[] nums = countBits(6); 7 for (int i = 0; i < nums.length; i++) { 8 System.out.print(nums[i] + " "); 9 } 10 } 11 12 public static int[] countBits(int num) { 13 int[] temp = new int[num+1]; 14 for (int i = 1; i <= num; i++) { 15 temp[i] = temp[i & (i - 1)] + 1; 16 } 17 return temp; 18 } 19 20 }