这一节,在熟悉了Featue maps相关概念之后,我们将开始学习基于EKF的特征图SLAM算法。
1. 机器人,图和增强的状态向量
随机SLAM算法一般存储机器人位姿和图中的地标在单个状态向量中,然后通过一个递归预测和量测过程来估计状态参数。其中,预测阶段通过增量航迹估计来处理机器人的运动,并增加了机器人位姿不确定性的估计。当再次观测到Map中存储的特征后,量测阶段,或者叫更新阶段开始执行,这个过程可以改善整个的状态估计。当机器人在运动过程中观测到新特征时,便通过一个状态增强的过程将新观测的特征添加到状态向量中。
机器人的状态,即一个相对于参考笛卡尔坐标系的自身位姿参数通过均值和协方差来定义:
 (1)
(1)
 (2)
(2)
图的协方差矩阵Pm 包含特征之间的互相关信息(即非对角项),这些交叉关联信息表征了每个特征对Map中其他特征相关信息的依赖。由于特征的位置是静态的,当周围的环境也即Map是刚性的话,特征之间的交叉关联将会随着的特征的二次观测增强。图中的特征可以表示如下
 (3)
(3)
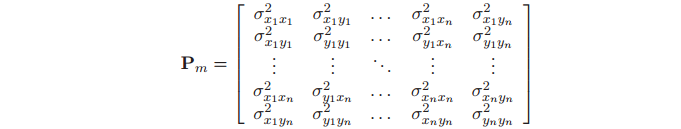 (4)
(4)
SLAM中的图通过一个串联了机器人位姿和特征图状态的增强状态向量定义,如图1所示。这是很有必要的,因为一致的SLAM依赖于机器人位姿和图之间相关性Pvm
 (5)
(5)
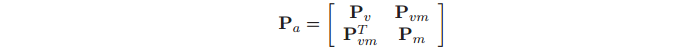 (6)
(6)

Fig. 1 增强的状态向量.
需要注意的是,状态的初始化时通常为 和
和 .也就是说,还没有特征被机器人观测到,并且初始时刻机器人位于参考坐标系的原点。
.也就是说,还没有特征被机器人观测到,并且初始时刻机器人位于参考坐标系的原点。
2. 预测阶段
随机SLAM算法的过程模型根据航迹推算运动估计来确定机器人相对于先前时刻位姿的运动,图特征仍然保持静止。这个模型对状态估计的影响存在于状态向量 部分和状态协方差矩阵中的
部分和状态协方差矩阵中的 以及
以及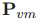 项。而
项。而 和
和 这些图特征相关项仍保持不变。
这些图特征相关项仍保持不变。
估计带来的机器人(这里以移动小车为例)位姿变化 和协方差
和协方差 通常用车轮的编码器测量和小车对应的运动学模型获取。本文里面的位姿改变通过基于激光测距的航迹推算获取,该算法可以通过批处理数据关联算法来找出序列激光扫描之间的相对位姿关系。
通常用车轮的编码器测量和小车对应的运动学模型获取。本文里面的位姿改变通过基于激光测距的航迹推算获取,该算法可以通过批处理数据关联算法来找出序列激光扫描之间的相对位姿关系。

Fig. 2 机器人位姿变化示意.
因此,预测的增强状态可以表示为
 (7)
(7)
 (8)
(8)
其中,雅各比矩阵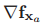 和
和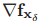 的定义为
的定义为
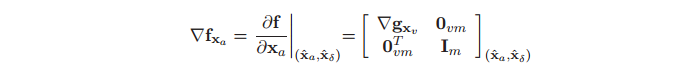 (9)
(9)
 (10)
(10)
雅各比矩阵 和
和 定义为
定义为
 (11)
(11)
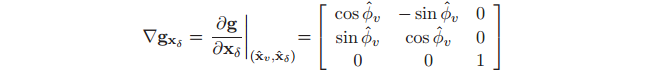 (12)
(12)
因为雅各比矩阵仅仅影响机器人的协方差矩阵 和对应的交叉相关性
和对应的交叉相关性 ,方程(8)用下式高效地实现
,方程(8)用下式高效地实现
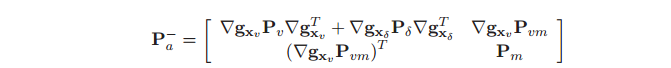 (13)
(13)
3. 更新阶段
如果已经存储在图中的估计特征 被距离方位传感器二次观测到,此时对应的量测量可以表示为
被距离方位传感器二次观测到,此时对应的量测量可以表示为
 (14)
(14)
 (15)
(15)
其中,量测量 分别表示对应的距离值和相对于观测机器人的偏转角度。
分别表示对应的距离值和相对于观测机器人的偏转角度。 为量测协方差。传感器获取的量测值和图之间的关联可以通过下面的方程表示
为量测协方差。传感器获取的量测值和图之间的关联可以通过下面的方程表示
 (16)
(16)
Kalman增益 可以得到
可以得到
 (17)
(17)![]() (18)
(18)
![]() (19)
(19)
其中,雅各比矩阵 为
为
 (20)
(20)
对于包含许多特征的SLAM图,雅各比矩阵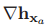 将会含有许多零项,这会使得方程(18)和(19)的计算非常高效。
将会含有许多零项,这会使得方程(18)和(19)的计算非常高效。
随后我们可以从更新过程得到一个后验SLAM估计
 (21/22)
(21/22)
实践表明,如果几个独立的量测同时可用,即知道 ,便有可能获取更加精确的更新。
,便有可能获取更加精确的更新。
4. 状态增强
当机器人在环境中漫游时,一旦新特征被观测到,就必须存储到图中。接下来将给出新观测到的特征初始化方法,首先,状态向量和对应的协方差矩阵通过新的量测的极值增强为
 (23)
(23)
 (24)
(24)
量测z 通过函数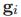 被转换位全局的笛卡尔坐标系特征位置,对应的变换表示如下
被转换位全局的笛卡尔坐标系特征位置,对应的变换表示如下
 (25)
(25)
可以通过线性化函数 将增强的状态初始化
将增强的状态初始化
 (26/27)
(26/27)
其中,雅克比矩阵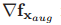 表示为
表示为
 (28)
(28)
与特征的储存相比,特征的删除非常简单,只需将特征对应的元素直接从状态向量删除,同时将相关的行和列中的项目从协方差矩阵中删除。