枚举入门。
原题链接:http://poj.org/problem?id=2029 POJ
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=716 ZOJ
Get Many Persimmon Trees
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 2788 | Accepted: 1808 |
Description
Seiji Hayashi had been a professor of the Nisshinkan Samurai School in the domain of Aizu for a long time in the 18th century. In order to reward him for his meritorious career in education, Katanobu Matsudaira, the lord of the domain of Aizu, had decided to
grant him a rectangular estate within a large field in the Aizu Basin. Although the size (width and height) of the estate was strictly specified by the lord, he was allowed to choose any location for the estate in the field. Inside the field which had also
a rectangular shape, many Japanese persimmon trees, whose fruit was one of the famous products of the Aizu region known as 'Mishirazu Persimmon', were planted. Since persimmon was Hayashi's favorite fruit, he wanted to have as many persimmon trees as possible
in the estate given by the lord.
For example, in Figure 1, the entire field is a rectangular grid whose width and height are 10 and 8 respectively. Each asterisk (*) represents a place of a persimmon tree. If the specified width and height of the estate are 4 and 3 respectively, the area surrounded by the solid line contains the most persimmon trees. Similarly, if the estate's width is 6 and its height is 4, the area surrounded by the dashed line has the most, and if the estate's width and height are 3 and 4 respectively, the area surrounded by the dotted line contains the most persimmon trees. Note that the width and height cannot be swapped; the sizes 4 by 3 and 3 by 4 are different, as shown in Figure 1.
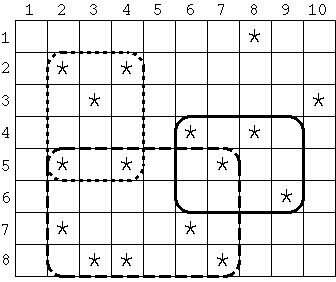
Figure 1: Examples of Rectangular Estates
Your task is to find the estate of a given size (width and height) that contains the largest number of persimmon trees.
For example, in Figure 1, the entire field is a rectangular grid whose width and height are 10 and 8 respectively. Each asterisk (*) represents a place of a persimmon tree. If the specified width and height of the estate are 4 and 3 respectively, the area surrounded by the solid line contains the most persimmon trees. Similarly, if the estate's width is 6 and its height is 4, the area surrounded by the dashed line has the most, and if the estate's width and height are 3 and 4 respectively, the area surrounded by the dotted line contains the most persimmon trees. Note that the width and height cannot be swapped; the sizes 4 by 3 and 3 by 4 are different, as shown in Figure 1.

Figure 1: Examples of Rectangular Estates
Your task is to find the estate of a given size (width and height) that contains the largest number of persimmon trees.
Input
The input consists of multiple data sets. Each data set is given in the following format.
N
W H
x1 y1
x2 y2
...
xN yN
S T
N is the number of persimmon trees, which is a positive integer less than 500. W and H are the width and the height of the entire field respectively. You can assume that both W and H are positive integers whose values are less than 100. For each i (1 <= i <= N), xi and yi are coordinates of the i-th persimmon tree in the grid. Note that the origin of each coordinate is 1. You can assume that 1 <= xi <= W and 1 <= yi <= H, and no two trees have the same positions. But you should not assume that the persimmon trees are sorted in some order according to their positions. Lastly, S and T are positive integers of the width and height respectively of the estate given by the lord. You can also assume that 1 <= S <= W and 1 <= T <= H.
The end of the input is indicated by a line that solely contains a zero.
N
W H
x1 y1
x2 y2
...
xN yN
S T
N is the number of persimmon trees, which is a positive integer less than 500. W and H are the width and the height of the entire field respectively. You can assume that both W and H are positive integers whose values are less than 100. For each i (1 <= i <= N), xi and yi are coordinates of the i-th persimmon tree in the grid. Note that the origin of each coordinate is 1. You can assume that 1 <= xi <= W and 1 <= yi <= H, and no two trees have the same positions. But you should not assume that the persimmon trees are sorted in some order according to their positions. Lastly, S and T are positive integers of the width and height respectively of the estate given by the lord. You can also assume that 1 <= S <= W and 1 <= T <= H.
The end of the input is indicated by a line that solely contains a zero.
Output
For each data set, you are requested to print one line containing the maximum possible number of persimmon trees that can be included in an estate of the given size.
Sample Input
16 10 8 2 2 2 5 2 7 3 3 3 8 4 2 4 5 4 8 6 4 6 7 7 5 7 8 8 1 8 4 9 6 10 3 4 3 8 6 4 1 2 2 1 2 4 3 4 4 2 5 3 6 1 6 2 3 2 0
Sample Output
4 3
Source
题意:给出一个矩形的长宽,在矩形中种树,给出树的位置。
再给你一个小矩形,用这个小矩形,框在这个大矩形中,问最多能框进去多少棵树。
思路:题目数据较小,从左到右,从上到下枚举下去即可。
样例分析:第一行N表示树的数目。
第二行W和H表示矩形的宽和高。
下面N行表示N棵树的位置。
最后一行S和T表示小矩形的宽和高。
注意:宽和高不可以颠倒位置。
#include<stdio.h>
#include<string.h>
int map[110][110];
int main()
{
int n,w,h,x,y,s,t;
int i,j,k,e,sum,max;
while(scanf("%d",&n)!=EOF && n)
{
sum=max=0;
memset(map,0,sizeof(map));
scanf("%d%d",&w,&h);
for(i=0;i<n;i++)
{
scanf("%d%d",&x,&y);
map[x][y]=1;//标记树的位置
}
scanf("%d%d",&s,&t);
for(i=0;i<=w-s+1;i++)
{
for(j=0;j<=h-t+1;j++)
{
sum=0;//初始化
for(k=i;k<=i+s-1;k++)
{
for(e=j;e<=j+t-1;e++)
{
if(map[k][e]) sum++;
}
}
max=max>sum?max:sum;
}
}
printf("%d\n",max);
}
return 0;
}