绘制二维图形的其它方案

1 其他形式的线性直角坐标图

　　在线性直角坐标系中，其他形式的图形有条形图、阶梯图、杆图和填充图等，所采用的函数分别是：

bar(x,y,选项)%条形图

stairs(x,y,选项)%阶梯图

stem(x,y，选项)%杆图

前3个函数的用法与plot函数相似，但没有多输入变量形式。

fill(x1,y1,选项1，x2，y2，选项2...)%填充图

fill函数按向量元素下标渐增次序用直线段连接x,y对应元素定义的数据点。假如这样连接所得拆线不封闭，那么MATLAB将自动 把该 拆线的首尾连接起来，构成封闭多边形。然后将多边形内部涂满指定的颜色。

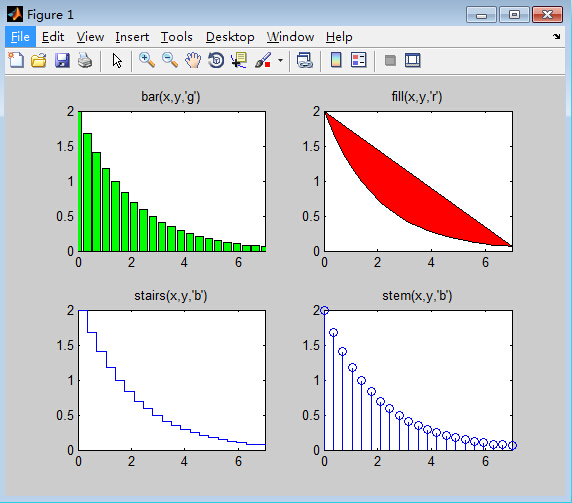
　　例5.8 分别以条形图，填充图、阶梯图和杆图形式绘制曲线y=2e(-0.5x)。

程序如下：

x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(2,2,1);
bar(x,y,'g');
title('bar(x,y,''g'')');
axis([0,7,0,2]);
subplot(2,2,2);
fill(x,y,'r');
title('fill(x,y,''r'')');
axis([0,7,0,2]);
subplot(2,2,3);
stairs(x,y,'b');
title('stairs(x,y,''b'')');
axis([0,7,0,2]);
subplot(2,2,4);
stem(x,y,'b');
title('stem(x,y,''b'')');
axis([0,7,0,2]);

　　　　

　　

2 极坐标图

polar函数用来绘制极坐标图，其调用格式为：

polar（theta，rho，选项）

其中，theta为坐标极角，rho为极坐标失径，选项的内容与plot函数相似。

例5.9 绘制p=sin（2theta）cos(2theta)的坐标图。
程序如下：
theta=0:0.01:2*pi;
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho,'k');

　　

3 对数坐标图

实际应用中，经常用到对数坐标，例如控制理论中的Bode图。MATLAB提供了绘制对数和半对数坐标曲线的函数，调用格式为：

semilogx(x1,y1,选项1，x2,y2,选项2，......)

semilogy(x1,y1,选项1，x2,y2,选项2，......)

loglog(x1,y1,选项1，x2,y2,选项2,......)

其中，选项的定义与plot函数完全一致，所不同的是坐标轴的选取。semilogx函数使用半对数坐标，x轴为常用对数刻度，而y轴仍保持线性刻度。semilogy函数也使用半对数坐标,y轴为常用对数刻度 ，x轴仍保持线性刻度。loglog函数使用全对数坐标，x、y轴均采用常用对数刻度。

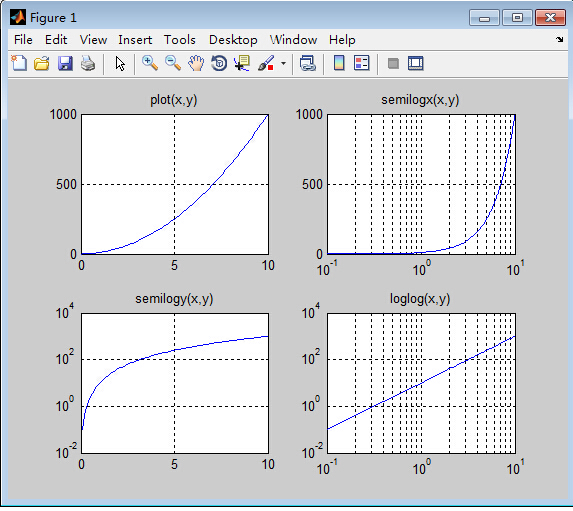
例：绘制y=10x^2的对数坐标图，并与直角线性坐标图进行比较。
程序如下：
x=0:0.1:10;
y=10*x.*x;
subplot(2,2,1);
plot(x,y);
title('plot(x,y)');grid on;
subplot(2,2,2);
semilogx(x,y);
title('semilogx(x,y)');grid on;
subplot(2,2,3);
semilogy(x,y);
title('semilogy(x,y)');grid on;
subplot(2,2,4);
loglog(x,y);
title('loglog(x,y)');grid on;

　　

MATLAB还提供了了一个实用的函数logspace，它可以按对数等间距地分布来产生一个向量。调用格式为：

logspace(a,b,n)

其中，a和b是生成向量的第一个和最后一个元素，n是元素总数。n省略时，自动产生50个元素。

4 其它形式的二维图形（饼图，向量图）

　　

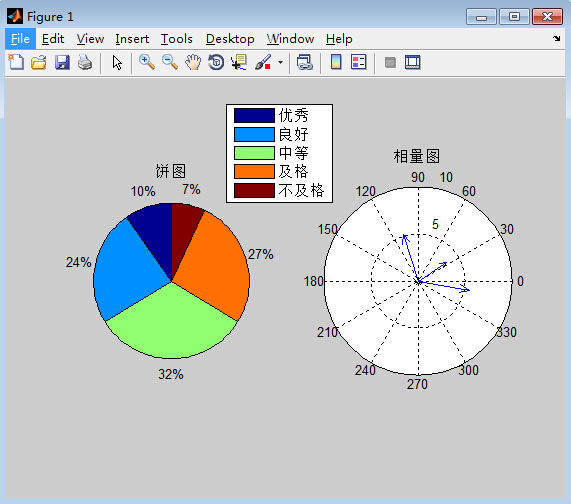
1    某次考试优秀、良好、中等、及格、不及格的人数分别为：7，17，23，19，5，试用饼图进行成绩统计分析。
2    绘制复数的相量图：3+2i,5.5-i和-1.5+5i.
程序如下：
subplot(1,2,1);
pie([7,17,23,19,5]);
title('饼图');
legend('优秀','良好','中等','及格','不及格');
subplot(1,2,2);
compass([3+2i,5.5-i,-1.5+5i]);
title('相量图');