Problem:
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
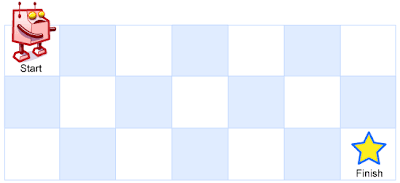
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Analysis:
It is a simple DP problem. Assume Smn is the number of unique paths when the grid is m*n.
Then Smn = S(m-1)n + Sm(n-1). If simply coding it, it will has Time Limit Exceeded error due to the many recomputations.
S(23, 12) = S(22, 12) + S(23, 11)
= S(21, 12) + S(22, 11) + S(22, 11) + S(23, 10) // rep 1
= S(20, 12) + S(21, 11) + S(21, 11) + S(22, 12) +S(21, 11) + S(22, 10) + S(22, 10) + S(23, 9) //rep 3
= ....
The time complxity here may be expotential.
So we need to use a bottom-up method which compute base cases first and store the result into the table for future reference.
The time complexity is only O(m*n)
Code:

1 class Solution { 2 public: 3 int uniquePaths(int m, int n) { 4 // Start typing your C/C++ solution below 5 // DO NOT write int main() function 6 int tab[m][n]; 7 8 for (int i=0; i<m; i++) 9 for (int j=0; j<n; j++) { 10 if (i == 0 || j == 0) 11 tab[i][j] = 1; 12 else 13 tab[i][j] = -1; 14 } 15 16 for (int i=1; i<m; i++) { 17 for (int j=1; j<n; j++) { 18 if (tab[i][j] == -1) 19 tab[i][j] = tab[i-1][j] + tab[i][j-1]; 20 } 21 } 22 23 return tab[m-1][n-1]; 24 } 25 };
Attention:
