向量数量积的坐标公式为什么是横纵坐标分别相乘之和
(横坐标相乘加上纵坐标相乘)
有同学认为这个证明有循环论证之嫌,即先用数量积坐标公式证明余弦定理,又用了余弦定理反过来证明这个公式,这里添加一些步骤来说明这个问题。想看推导坐标公式的同学可以直接跳过这一段看分割线后面的部分。
定义1: 两向量的数量积定义为其中一条向量在另一条向量方向上的正投影的长度与被投影向量的长度之积,若投影出的向量与被投影向量方向一致则此值为正,若相反则此值为负。即:\(\vec{u}\cdot \vec{v}= \vec{v}\cdot \vec{u}= \left | \vec{u} \right | \cdot \left | \vec{v} \right | \cdot \cos \left \langle \vec{u}, \vec{v} \right \rangle\).其中\(\left \langle \vec{u}, \vec{v} \right \rangle\)代表两向量的夹角。
定理1: 向量数量积的乘法分配律,即:\(\vec{a} \cdot \left ( \vec{u} + \vec{v} \right )= \vec{a} \cdot\vec{u}+\vec{a} \cdot \vec{v}\)
证明:如图,设 \(\overrightarrow{AD} = \vec{a},\overrightarrow{AB} = \vec{u},\overrightarrow{BC} = \vec{v},\overrightarrow{AC} = \vec{w}= \vec{u}+ \vec{v}\)
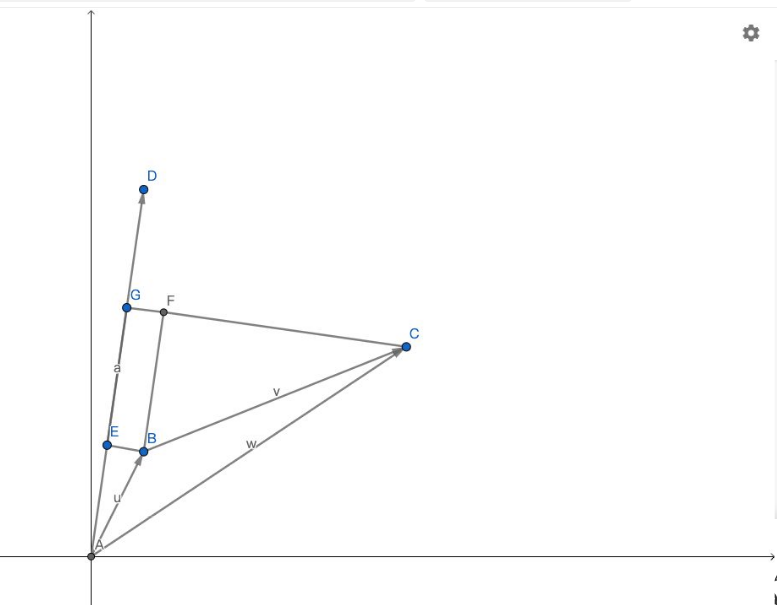
即证: \(\vec{a}\cdot\vec{w}=\vec{a}\cdot\vec{u}+\vec{a}\cdot\vec{v}\)
分别过B、C作AD的垂线,垂足分别为E、G. 再过B作CG的垂线,垂足为F .
易知 $ \vec{a} \cdot \vec{w} = \left | AD \right |\cdot \left | AG \right |,
\vec{a} \cdot \vec{u} = \left | AD \right |\cdot \left | AE \right |,
\vec{a} \cdot \vec{v} = \left | AD \right |\cdot \left | BF \right | = \left | AD \right |\cdot \left | EG \right |.$
又\(\left | AG \right | = \left | AE \right | + \left | EG \right |\) 故 \(\left | AD \right | \cdot \left | AG \right | = \left | AD \right | \cdot \left ( \left | AE \right | + \left | EG \right | \right )\)
即:\(\vec{a}\cdot\vec{w}=\vec{a}\cdot\vec{u}+\vec{a}\cdot\vec{v}\)
证毕
由定理1容易得到:
\begin{split}
{\left ( \vec{u} +\vec{v} \right )}^2 \newline
& =\left ( \vec{u} +\vec{v} \right )\cdot \left ( \vec{u} +\vec{v} \right ) \newline
& = \vec{u}^2 +2\vec{u}\cdot \vec{v}+ \vec{v}^2
\end{split}
定理2(余弦定理): 在\(\bigtriangleup ABC\)中,设\(\angle A\)所对的边长为\({a}\), \(\angle B\)所对的边长为\({b}\), \(\angle C\)所对的边长为\({c}\)
, 则它们满足如下关系:
\begin{split}
\newline
&{a}^2 + {b}^2 - {c}^2 = 2{a}{b}\cdot \cos C \newline
&{b}^2 + {c}^2 - {a}^2 = 2{b}{c}\cdot \cos A \newline
&{a}^2 + {c}^2 - {b}^2 = 2{a}{c}\cdot \cos B \newline
\end{split}
证毕
由此可见余弦定理可以直接作为向量数量积定义的一个推论而并没有涉及到数量积的坐标公式(就是下面证的这个),因此并不存在循环论证的问题。当然余弦定理不止这一种证法,其他方法有兴趣的话可以自行研究。
以下为原回答
向量数量积的坐标公式,应该是说下面这个:
向量\(\vec{u} = \left ( x_{1},y_{1} \right ),\vec{v} = \left ( x_{2},y_{2} \right )\),则\(\vec{u}\cdot \vec{v} = x_{1}x_{2}+y_{1}y_{2}\)
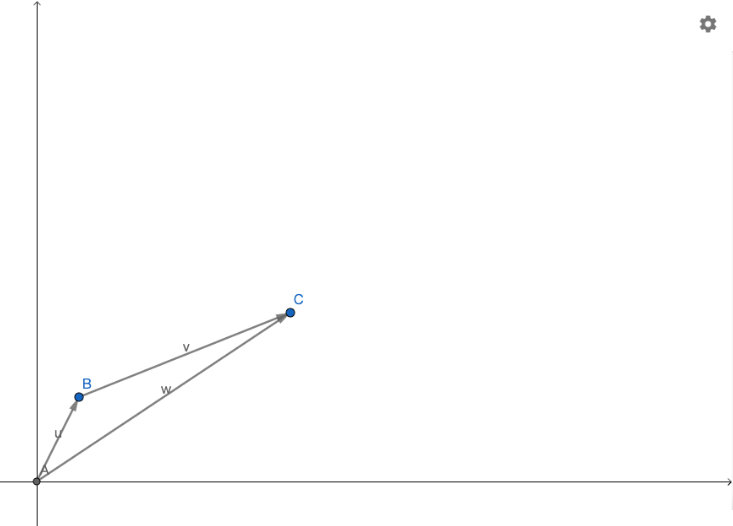
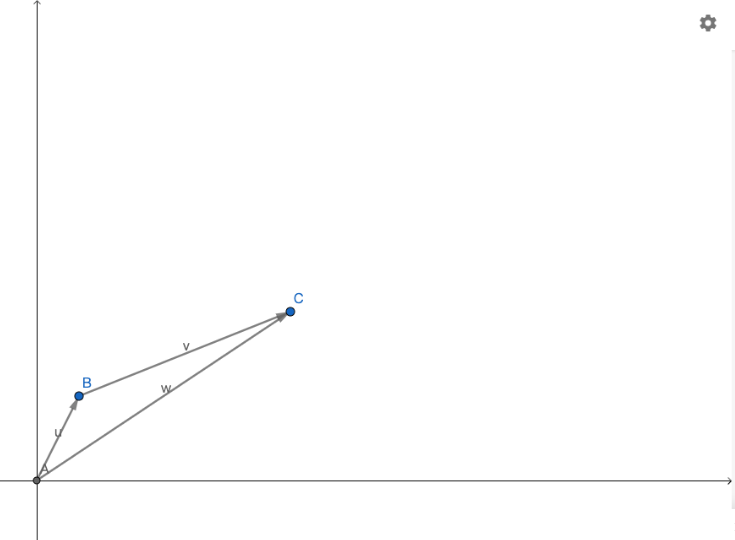
用\(\theta\)表示两向量的夹角,则它们的数量积即为\(\left | \vec{u} \right |\cdot \left | \vec{v} \right |\cdot \cos \theta\),且$\angle ABC = \pi - \theta $ .接下来就是求\(\cos \theta\)的问题。
由余弦定理,设$\left |\vec{u} \right | = {a},\left |\vec{v} \right | = {b},\left |\vec{w} \right | = {c}$,则\begin{split}
\newline
&\cos \left(\pi-\theta \right)=\frac{{a}^2 + {b}^2 - {c}^2}{2ab} \newline
&=\frac{x_{1}^{2} + y_{1}^{2} + x_{2}^{2} + y_{2}^{2} - \left ( x_{1} + x_{2} \right )^{2} - \left ( y_{1} + y_{2} \right )^{2}}{2ab} \newline
&=\frac{x_{1}x_{2} + y_{1}y_{2} }{ab} \newline
\end{split}
所以:
\(\cos \theta =\frac{x_{1}x_{2} + y_{1}y_{2} }{ab}\)
代入数量积公式,分母约掉即可得到结果。
以下是另一思路:

转 : https://www.zhihu.com/question/354296745?utm_id=0
数学公式:https://latex.codecogs.com/eqneditor/editor.php