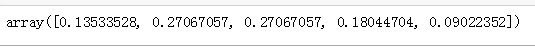推论统计学是数据分析、机器学习的基石
第一部分:总体的2种商业模式分式
什么是概率分布?
概率分布,是指用于表述随机变量取值的概率规律。
事件的概率表示了一次试验中某一个结果发生的可能性大小。
若要全面了解试验,则必须知道试验的全部可能结果及各种可能结果发生的概率,即随机试验的概率分布。
如果试验结果用变量X的取值来表示,则随机试验的概率分布就是随机变量的概率分布,即随机变量的可能取值及取得对应值的概率。
根据随机变量所属类型的不同,概率分布取不同的表现形式。
随机变量
随机变量(random variable)表示随机试验各种结果的实值单值函数。
随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
分为离散随机变量和连续随机变量
离散型
离散型(discrete)随机变量即在一定区间内变量取值为有限个或可数个。
例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。
离散型随机变量通常依据概率质量函数分类,主要分为:伯努利随机变量、二项随机变量、几何随机变量和泊松随机变量。
连续型
连续型(continuous)随机变量即在一定区间内变量取值有无限个,或数值无法一一列举出来。
例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
有几个重要的连续随机变量常常出现在概率论中,如:均匀随机变量、指数随机变量、伽马随机变量和正态随机变量。
离散型随机变量的概率计算公式为概率质量函数(PMF),统计图中的形状为离散概率分布
连续型随机变量的概率计算公式为概率密度函数(PDF),统计图中的形状为连续概率分布
离散概率分布
离散随机变量(概率质量函数PMF),其中常见的包括伯努利分布、二项分布、几何分布和泊松分布
一、伯努利分布(0-1分布)
#导入包 #数组包 import numpy as np #绘图包 import matplotlib.pyplot as plt #统计计算包的统计模块 from scipy import stats
''' arange用于生成一个等差数组,arange([start, ]stop, [step, ] 使用见文档:https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html ''' ''' 第1步,定义随机变量:1次抛硬币 成功指正面朝上记录为1,失败指反面朝上记录为0 ''' X = np.arange(0, 2,1) X
''' 伯努利分布官方使用文档: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.bernoulli.html#scipy.stats.bernoulli ''' #第2步,#求对应分布的概率:概率质量函数 (PMF) #它返回一个列表,列表中每个元素表示随机变量中对应值的概率 p = 0.5 # 硬币朝上的概率 pList = stats.bernoulli.pmf(X, p) pList
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码
#第3步,绘图 ''' plot默认绘制折线,这里我们只绘制点,所以传入下面的参数: marker:点的形状,值o表示点为圆圈标记(circle marker) linestyle:线条的形状,值None表示不显示连接各个点的折线 ''' plt.plot(X, pList, marker='o',linestyle='None') ''' vlines用于绘制竖直线(vertical lines), 参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值) 我们传入的X是一个数组,是给数组中的每个x坐标值绘制竖直线, 竖直线y坐标最小值是0,y坐标值最大值是对应pList中的值 官网文档:https://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.vlines ''' plt.vlines(X, 0, pList) #x轴文本 plt.xlabel('随机变量:抛硬币1次') #y轴文本 plt.ylabel('概率') #标题 plt.title('伯努利分布:p=%.2f' % p) #显示图形 plt.show()
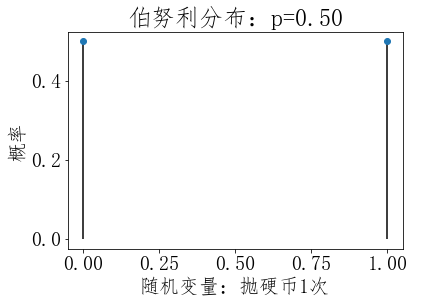
二项分布(Binomial Distribution)
二项分布即重复N次独立的伯努利分布,二项分布求出的结果即某事件发生x次的概率
p表示成功的概率;k表示想知道成功的次数。P(X=k)=C(n,k)(p^k)*(1-p)^(n-k)。
#导入包 #数组包 import numpy as np #绘图包 import matplotlib.pyplot as plt #统计计算包的统计模块 from scipy import stats
''' arange用于生成一个等差数组,arange([start, ]stop, [step, ] 使用见文档:https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html ''' #第1步,定义随机变量:5次抛硬币,正面朝上的次数 n = 5 # 做某件事情的次数 p = 0.5 # 做某件事情成功的概率 X = np.arange(0, n+1,1) X
'''
二项分布官方使用文档:
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binom.html#scipy.stats.binom
'''
#第2步,#求对应分布的概率:概率质量函数 (PMF)
#它返回一个列表,列表中每个元素表示随机变量中对应值的概率
pList = stats.binom.pmf(X, n, p)
pList

"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码
#第3步,绘图 ''' plot默认绘制折线,这里我们只绘制点,所以传入下面的参数: marker:点的形状,值o表示点为圆圈标记(circle marker) linestyle:线条的形状,值None表示不显示连接各个点的折线 ''' plt.plot(X, pList, marker='o',linestyle='None') ''' vlines用于绘制竖直线(vertical lines), 参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值) 我们传入的X是一个数组,是给数组中的每个x坐标值绘制竖直线, 竖直线y坐标最小值是0,y坐标值最大值是对应pList中的值 官网文档:https://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.vlines ''' plt.vlines(X, 0, pList) #x轴文本 plt.xlabel('随机变量:抛硬币正面朝上次数') #y轴文本 plt.ylabel('概率') #标题 plt.title('二项分布:n=%i,p=%.2f' % (n,p)) #显示图形 plt.show()
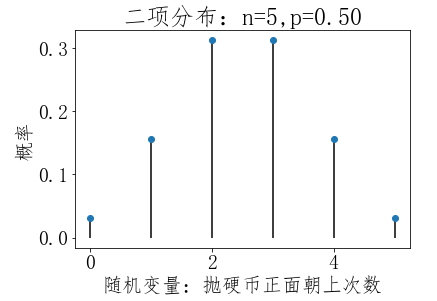
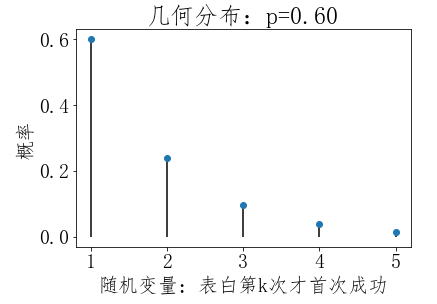
几何分布(Geometric Distribution)
几何分布同样以伯努利分布为基础,即在N次伯努利分布试验中,试验k次才第一次获得成功的概率
#导入包 #数组包 import numpy as np #绘图包 import matplotlib.pyplot as plt #统计计算包的统计模块 from scipy import stats
''' arange用于生成一个等差数组,arange([start, ]stop, [step, ] 使用见文档:https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html ''' ''' 第1步,定义随机变量: 首次表白成功的次数,可能是1次,2次,3次等 ''' #第k次做某件事情,才取到第1次成功 #这里我们想知道5次表白成功的概率 k = 5 # 做某件事情成功的概率,这里假设每次表白成功概率都是60% p = 0.6 X = np.arange(1, k+1,1) X
''' 几何分布官方使用文档: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.geom.html#scipy.stats.geom ''' #第2步,#求对应分布的概率:概率质量函数 (PMF) #它返回一个列表,列表中每个元素表示随机变量中对应值的概率 #分别表示表白第1次才成功的概率,表白第2次才成功的概率,表白第3次才成功的概率,表白第4次才成功的概率,表白第5次才成功的概率 pList = stats.geom.pmf(X,p) pList
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码
#第3步,绘图 ''' plot默认绘制折线,这里我们只绘制点,所以传入下面的参数: marker:点的形状,值o表示点为圆圈标记(circle marker) linestyle:线条的形状,值None表示不显示连接各个点的折线 ''' plt.plot(X, pList, marker='o',linestyle='None') ''' vlines用于绘制竖直线(vertical lines), 参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值) 我们传入的X是一个数组,是给数组中的每个x坐标值绘制竖直线, 竖直线y坐标最小值是0,y坐标值最大值是对应pList中的值 官网文档:https://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.vlines ''' plt.vlines(X, 0, pList) #x轴文本 plt.xlabel('随机变量:表白第k次才首次成功') #y轴文本 plt.ylabel('概率') #标题 plt.title('几何分布:p=%.2f' % p) #显示图形 plt.show()
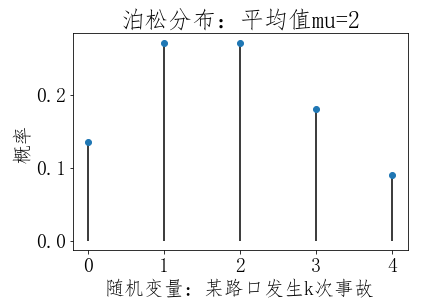
泊松分布(Poisson Distribution)
一个事件在一段时间内随机发生,其服从泊松分布的条件为:
(1)将该时间段无限分隔成很多个小的时间段,在这个小的时间段内,事件发生的概率非常小,不发生的概率非常大。
(2)在每个小的时间段内,事件发生的概率是稳定的,且与小的时间段的长度成正比。
(3)该事件在不同的小时间段里,发生与否相互独立。
#导入包 #数组包 import numpy as np #绘图包 import matplotlib.pyplot as plt #统计计算包的统计模块 from scipy import stats
''' arange用于生成一个等差数组,arange([start, ]stop, [step, ] 使用见文档:https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html ''' ''' 第1步,定义随机变量: 已知某路口发生事故的比率是每天2次, 那么在此处一天内发生k次事故的概率是多少? ''' mu = 2 # 平均值:每天发生2次事故 k=4 #次数,现在想知道每天发生4次事故的概率 #包含了发生0次、1次、2次,3次,4次事故 X = np.arange(0, k+1,1) X
''' 泊松分布官方使用文档: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.poisson.html#scipy.stats.poisson ''' #第2步,#求对应分布的概率:概率质量函数 (PMF) #它返回一个列表,列表中每个元素表示随机变量中对应值的概率 #分别表示发生1次,2次,3次,4次事故的概率 pList = stats.poisson.pmf(X,mu) pList
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码
#第3步,绘图 ''' plot默认绘制折线,这里我们只绘制点,所以传入下面的参数: marker:点的形状,值o表示点为圆圈标记(circle marker) linestyle:线条的形状,值None表示不显示连接各个点的折线 ''' plt.plot(X, pList, marker='o',linestyle='None') ''' vlines用于绘制竖直线(vertical lines), 参数说明:vline(x坐标值, y坐标最小值, y坐标值最大值) 我们传入的X是一个数组,是给数组中的每个x坐标值绘制竖直线, 竖直线y坐标最小值是0,y坐标值最大值是对应pList中的值 官网文档:https://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.vlines ''' plt.vlines(X, 0, pList) #x轴文本 plt.xlabel('随机变量:某路口发生k次事故') #y轴文本 plt.ylabel('概率') #标题 plt.title('泊松分布:平均值mu=%i' % mu) #显示图形 plt.show()
连续型随机变量
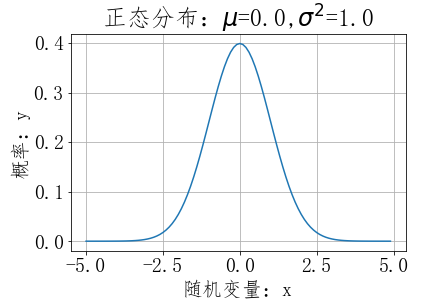
正态分布(Normal Distribution)
正态分布属于连续型随机变量,若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
#导入包 #数组包 import numpy as np #绘图包 import matplotlib.pyplot as plt #统计计算包的统计模块 from scipy import stats
''' arange用于生成一个等差数组,arange([start, ]stop, [step, ] 使用见文档:https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html ''' ''' 第1步,定义随机变量: ''' mu=0 #平均值 sigma= 1 #标准差 X = np.arange(-5, 5,0.1) X
#第2步,概率密度函数(PDF) y=stats.norm.pdf(X,mu,sigma)
"""设置字体,用于显示中文""" plt.rcParams['font.sans-serif']=['FangSong'] """SimSun 宋体,Microsoft YaHei微软雅黑 YouYuan幼圆 FangSong仿宋""" plt.rcParams['font.size']=20 plt.rcParams['axes.unicode_minus']=False# 负号乱码
#第3步,绘图 ''' plot默认绘制折线 ''' plt.plot(X, y) #x轴文本 plt.xlabel('随机变量:x') #y轴文本 plt.ylabel('概率:y') #标题 plt.title('正态分布:$mu$=%.1f,$sigma^2$=%.1f' % (mu,sigma)) #网格 plt.grid() #显示图形 plt.show()
概率分布对数据分析、机器学习有什么用?
什么是幂律分布?
某个具有分布性质的变量,只要其分布密布函数是幂函数(由于分布密度函数必然满足“归一律”,所以这里的幂函数,一般规定小于负1),都可以称其满足幂律分布规律。
这个定义是很清晰的,没有多种解释。这种分布是自然界中的一种常见现象。
譬如地震的大小,通常震级越小发生的频率越大,震级越大发生的频率就越小。
以震级为自变量,以其发生的频率(或概率)为因变量,符合(负)幂函数。
一般地,y=xα(α为有理数)的函数,即以底数为自变量,幂为因变量,指数为常数的函数称为幂函数。
例如函数y=x0 、y=x1、y=x2、y=x-1(注:y=x-1=1/x、y=x0时x≠0)等都是幂函数。
如何选择你的人生商业模式,才能离财务自由更近
第一种:同一份时间出售一次
第二种:重复出售同一份时间
第三种:购买他人的时间再出售