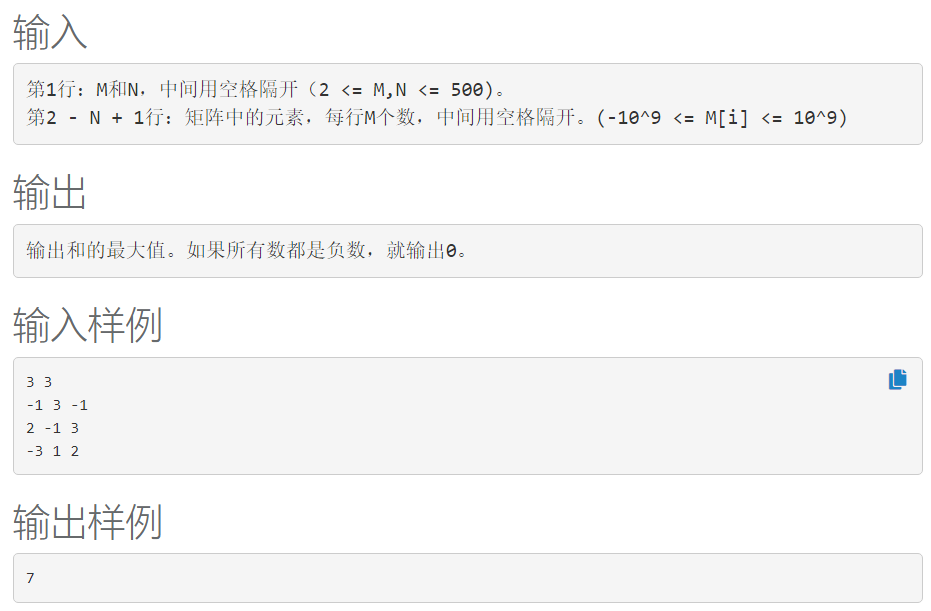
题面:

为一维字段和最大值的二维拓展版;
考虑固定右下端点(i,j)然后固定子矩阵的高度为k,那么就可以转化为一维的最大字段和。
空间可以优化到0(n)
时间复杂度o(n^3)

#include<bits/stdc++.h> #define ll long long using namespace std; const int N=510; ll dp[N],a[N][N]; int main() { int n,m; cin>>m>>n; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%lld",&a[i][j]),a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1]; ll ans=0; for(int i=1;i<=n;i++) { for(int k=1;k<=i;k++) { dp[k]=0; for(int j=1;j<=m;j++) { ll s=a[i][j]-a[i-k][j]-a[i][j-1]+a[i-k][j-1]; if(dp[k]>0) dp[k]+=s; else dp[k]=s; //dp[k]=max(dp[k]+s,s); ans=max(ans,dp[k]); } } } cout<<ans<<endl; return 0; }
