博客转载自:https://blog.csdn.net/crescent__moon/article/details/16986765
先说说Dijkstra吧,这种算法只能求单源最短路径,那么什么是单源最短路径呢?就是只能求一个点到别的点最短路径,而不能求所有点到其它点的最短路径。当然如果枚举所有点都用一遍Dijkstra的话,也能求出来,不过这就失去了这个算法的真正意义,而且时间复杂度会从O(n^2)变为O(n^3)。这个算法还有一个缺点就是在图中权值必须都是正的,否则不能用。下面说说Dijkstra的实现,首先你得有一个要求的源点和终点,然后有图,如果图之间没有直接连边,则初始化它们的权值为inf,如果两点相同,则权值为0,当然这是用邻接矩阵存的图,确保存的边是最短的。然后你得有两个数组来维护,一个是vis数组,用来判断节点是否被访问过,另一个是dis数组,用来存储其余点到源点的最短路径。初始化时,将vis数组全部设为false,dis数组为图中源点到各个点的距离,如果没有直接路径,则为inf。好了,初始化结束了,要开始实现了,要确保每个点都被访问过,所以除了源点之外,还有n-1个点,所以要遍历这n-1个点。每一次从这些点中找出vis是false的,也就是没有被访问过的,而且从这些中在找出到源点最近的那个点,设为v,然后标记v的vis为true,然后以这个v点开始,遍历与p点相邻的点,并且这些相邻的的点还要确保都没有访问过(vis为false)。然后这个算法关键之处就到来了,对这些与v相邻的顶点设为w,依次判读dis[v]的值+c(v,w)(代表v到w的直接可达的路径)是否小于dis[w],如果小于,则更新dis[w]的值。至此为止,就是Dijksta算法。
以这个图为例来演示一遍这个算法的实现:以a为源点,求a到其它点的最短路径。
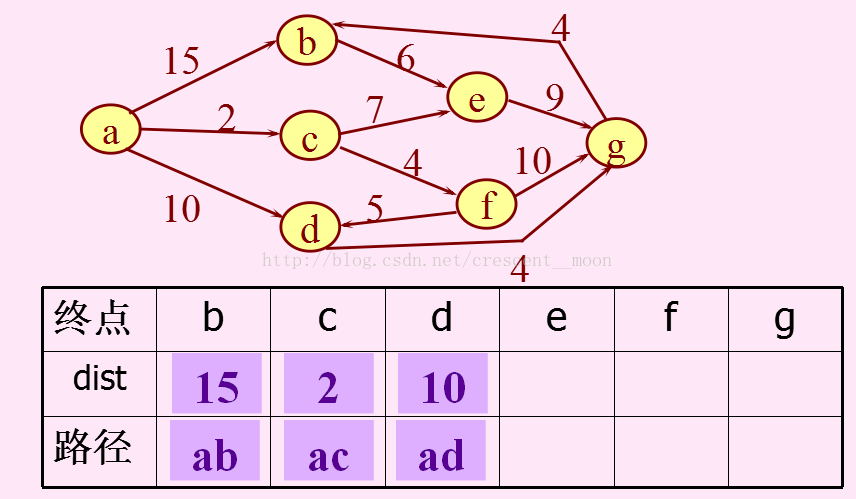
然后找与adist最近的,即c点,然后以c点开始遍历与其相邻的节点e和f,并更新它们的dist和路径。
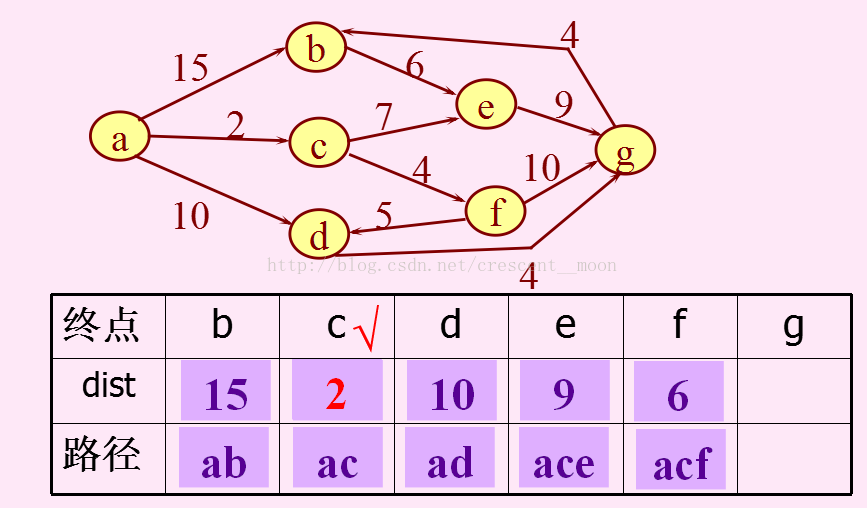
c点vis标记为true了,然后找vis标记为false的且dist最小的,也就是f点,遍历与f点相邻的邻接点且vis为false,也就是g和d点。

所以f点也访问完了,vis标记为true,然后接下来找的点,大家也能一眼看出是找e点了,然后遍历g点。

接下来访问d点。

在访问g点。
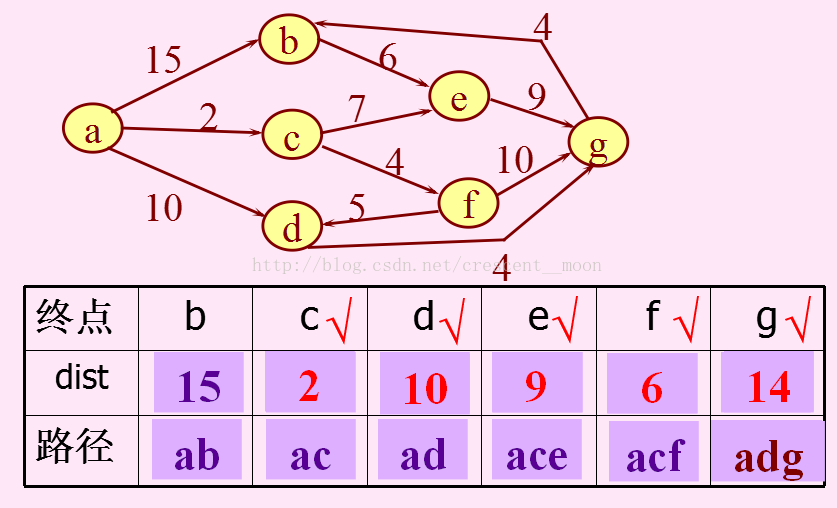
最后访问b点。
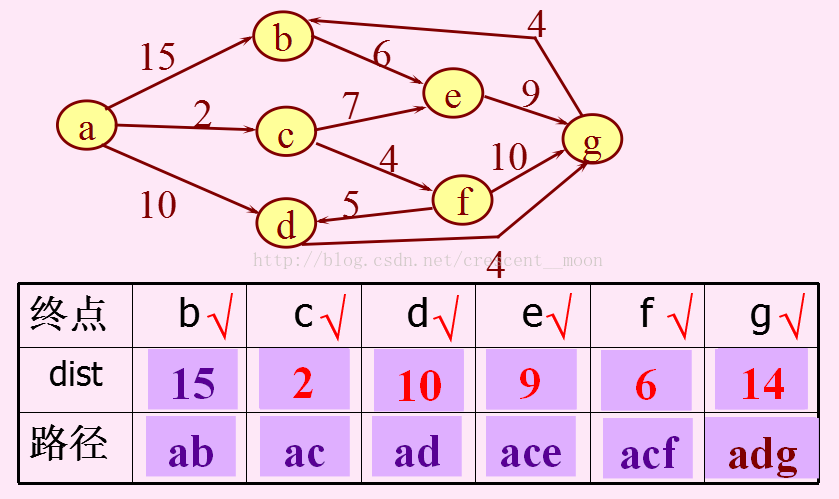
这就是此算法的实现。伪代码是:
void dijkstra(int u)//u为源点
{
for(int i=1; i<=n; i++)
{
dist[i]=map[u][i];
vis[i]=0;
}
dist[u]=0;
vis[u]=1;
for(int i=2; i<=n; i++)
{
int pos=0,min=inf;
for(j=1; j<=n; j++)
if(!vis[j]&&dist[j]<min)
{
pos=j;
min=dist[j];
}
vis[pos]=1;
for(j=1; j<=n; j++)
{
if(!vis[j]&&dis[j]>dis[pos]+map[pos][j])
{
dis[j]=dis[pos]+map[pos][j]
pre[j]=pos;//记录其前驱
}
}
}
}
Floyd算法求的是所有点之间的最短路径,并且可以处理权值为负值的边,时间复杂度为O(n^3)。
定义Dk,i,j为从vi到vj只使用v1,v2,…,vk作为中间顶点的最短路径的权。根据这个定义,D0,i,j=ci,j,其中若(vi,vj)不是该图的边,则ci,j=∞。并且,根据定义,D|v|,i,j是图中从vi到vj的最短路径。Floyd算法的基本思想是动态规划,1、求出顶点Vi和Vj不经过任何顶点的最短路径,路径的长度就是二者之间边的权重,表示为:P(0,i,j)=C(i,j)。
2、当求出P(k-1,i,j) 后,即Vi到Vj经过V1到Vk-1中的某些顶点的最短路径。则:Vi到Vj的中间经过V1到Vk中某些顶点的最短路径P(k,i,j)。
图的表示为:



下面以一个例子来说明它的实现:这是初始时的情况
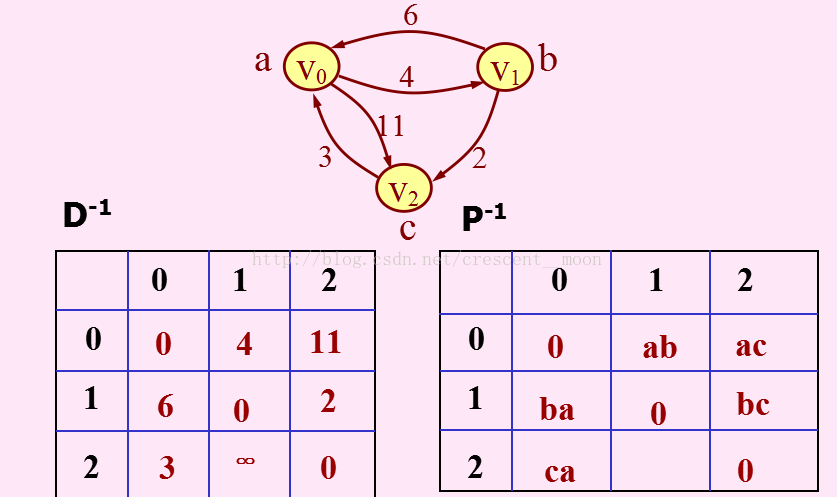
当k=0时,

当k=1时:
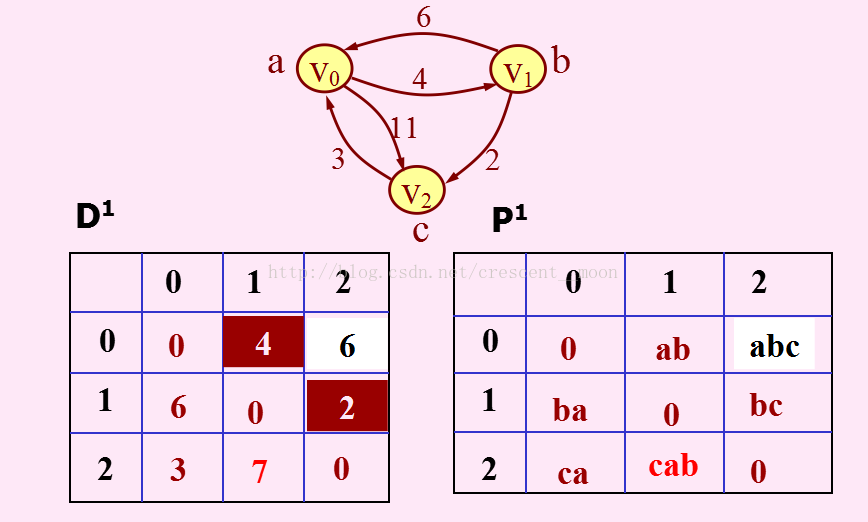
当k=2时:
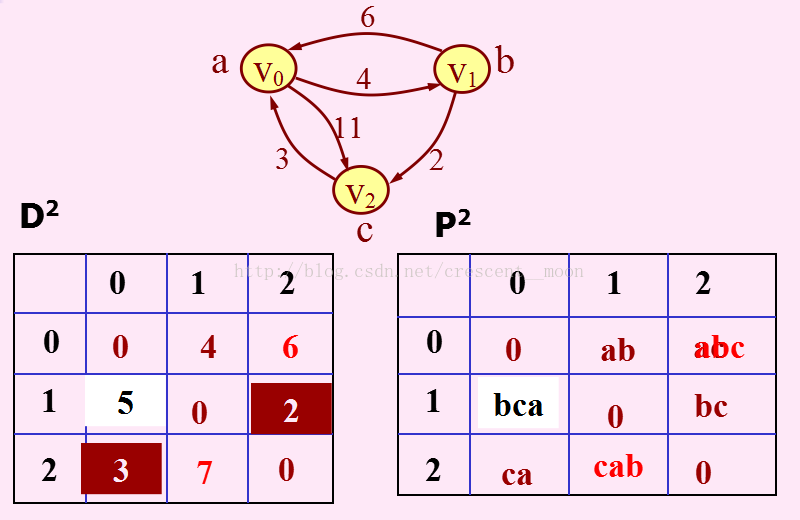
至此为止,此算法就结束了,图中的值即为任意两点间的最短距离。
Floyd的伪代码是:
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(map[i][k]+map[k][j]<map[i][j])
map[i][j]=map[i][k]+map[k][j];
}