博客转自:https://blog.csdn.net/aimeimeits/article/details/72809382
首先贝塞尔曲线简介,了解了基本的贝塞尔曲线知识之后,展开N阶贝塞尔曲线的生成方式。
N阶贝塞尔曲线的公式
百度百科上给出的一般参数公式是这样的:给定点 P0,P1,P2, … ,Pn,其贝塞尔曲线公式如下(即贝塞尔曲线上的点 B(t) 可由如下公式计算得到)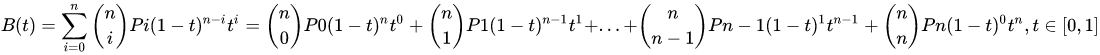
可以看出其公式是由一个格式固定的表达式之和来表示,这个表达式就是关键:
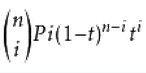
该表达式可分为四个部分看:
- 从 i 递增到 n 的常数部分
- Pi 坐标部分
- (1 - t)^(n - i)
- t^i
可以看出这四部分都与 i 的值相关,此外 t 值的计算方式为:i/(n+1)
可以从具体的例子中找到抽象规律
设 Bt 为要计算的贝塞尔曲线上的坐标,N 为控制点个数,P0,P1,P2..Pn 为贝塞尔曲线控制点的坐标,当 N 值不同时有如下计算公式: 如 N 为 3 表示贝塞尔曲线的控制点有 3 个点,这时 n 为 2 ,这三个点分别用 P0,P1,P2 表示。
- N = 3: P = (1-t)^2*P0 + 2*(1-t)*t*P1 + t^2*P2
- N = 4: P = (1-t)^3*P0 + 3*(1-t)^2*t*P1 + 3(1-t)*t^2*P2 + t^3*P3
- N = 5: P = (1-t)^4*P0 + 4*(1-t)^3*t*P1 + 6(1-t)^2*t^2*P2 + 4*(1-t)*t^3*P3 + t^4*P4
将贝塞尔曲线一般参数公式中的表达式用如下方式表示:设有常数 a,b 和 c,则该表达式可统一表示为如下形式
a * (1 - t)^b * t^c * Pn
分析当 N 分别为3,4,5 时对应 a,b,c 的值:如 N = 3 时,公式有三个表达式,第一个表达式为 (1-t)^2*P0,其对应 a,b,c 值分别为:1,2,0
N = 3: 1,2,0 2,1,1 1,0,2 a: 1 2 1 b: 2 1 0 c: 0 1 2 N = 4: 1,3,0 3,2,1 3,1,2 1,0,3 a: 1 3 3 1 b: 3 2 1 0 c: 0 1 2 3 N = 5: 1,4,0 4,3,1 6,2,2 4,1,3 1,0,4 a: 1 4 6 4 1 b: 4 3 2 1 0 c: 0 1 2 3 4
根据上面的分析就可以总结出 a,b,c 对应的取值规则:
- b: (N - 1) 递减到 0 (b 为 1-t 的幂)
- c: 0 递增到 (N - 1) (c 为 t 的幂)
- a: 在 N 分别为 1,2,3,4,5 时将其值用如下形式表示:
N=1:———1
N=2:——–1 1
N=3:——1 2 1
N=4:—–1 3 3 1
N=5:—1 4 6 4 1
a 值的改变规则为: 杨辉三角
C++实现代码
void n_bezier(int resolution) { int number = waypoints.size(); if (number < 2) { return; } int dimension = waypoints[0].size(); if (dimension < 2) { return; } std::vector<std::vector<double>> n_bezier_tmp_pts; //计算杨辉三角 std::vector<int> a_para; a_para.resize(number); a_para[0] = a_para[1] = 1; for (int i = 3; i <= number; i++) { std::vector<int> tmp; tmp.resize(i - 1); for (int j = 0; j < tmp.size(); j++) { tmp[j] = a_para[j]; } a_para[0] = a_para[i - 1] = 1; for (int j = 0; j < i - 2; j++) { a_para[j + 1] = tmp[j] + tmp[j + 1]; } } n_bezier_tmp_pts.resize(resolution); cv::Mat img_out; img.copyTo(img_out); //计算坐标点 for (int i = 0; i < resolution; i++) { float t = (float)i / resolution; n_bezier_tmp_pts[i].resize(dimension); for (int j = 0; j < dimension; j++) { float temp = 0.0f; for (int k = 0; k < number; k++) { temp += std::pow(1 - t, number - k - 1) * waypoints[k][j] * std::pow(t, k) * a_para[k]; } n_bezier_tmp_pts[i][j] = temp; } cv::circle(img_out, cv::Point2d(n_bezier_tmp_pts[i][0], n_bezier_tmp_pts[i][1]), 2, cv::Scalar(255, 0, 255), -1); } cv::imshow("spline", img_out); }
显示效果如下
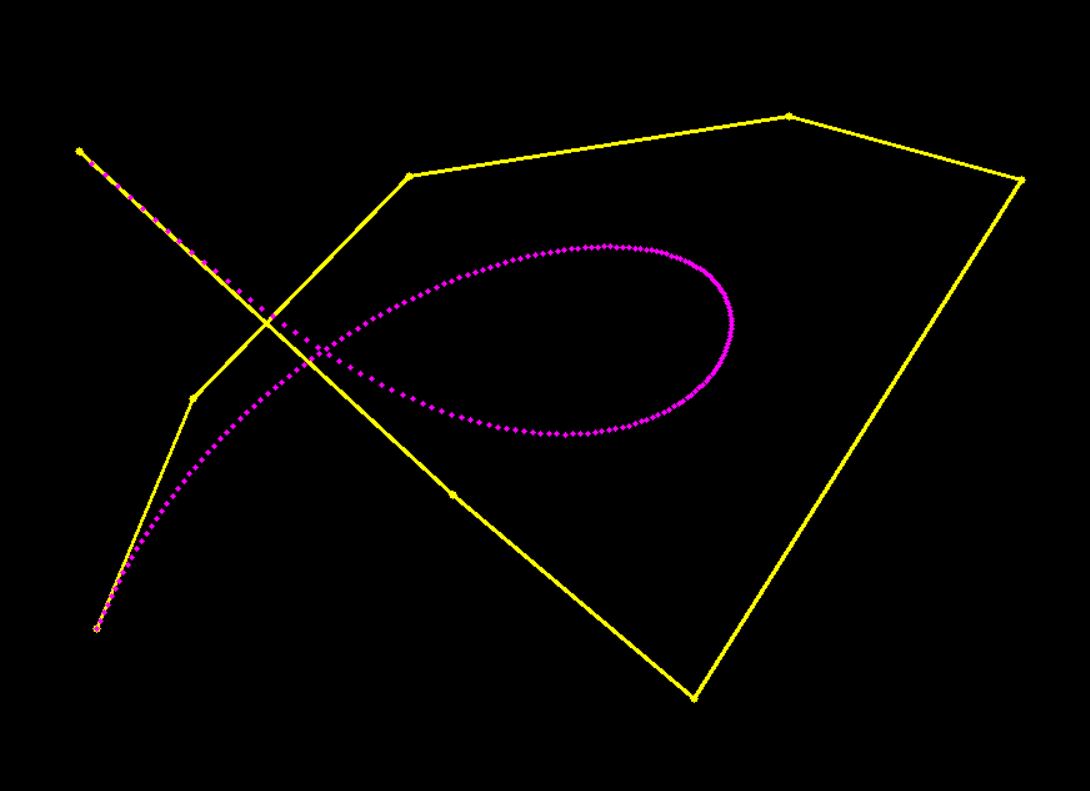
等有时间,整理完备,会更新到Githu