密码学系列之:生日攻击
简介
生日攻击其实是一个概率论的问题,也就是说一个看起来很难发生的事情,事实上它发生的概率却很大。这种主观上和事实上的概率差距,让随机攻击成功的几率变的更高,这样的攻击就叫做生日攻击。
生日问题的由来
生日问题也叫做生日悖论,它是这样这样描述的。
假如随机选择n个人,那么这个n个人中有两个人的生日相同的概率是多少。如果要想概率是100%,那么只需要选择367个人就够了。因为只有366个生日日期(包括2月29日)。
如果想要概率达到99.9% ,那么只需要70个人就够了。50%的概率只需要23个人。
对于现在的幼儿园小朋友来说,一个班上差不多有30人,那么将会有大于50%的几率,班上有两个人的生日是一样的。
听起来是不是很神奇?跟我们第一映像中的基数是不是要少很多。
我们看一张概率图:
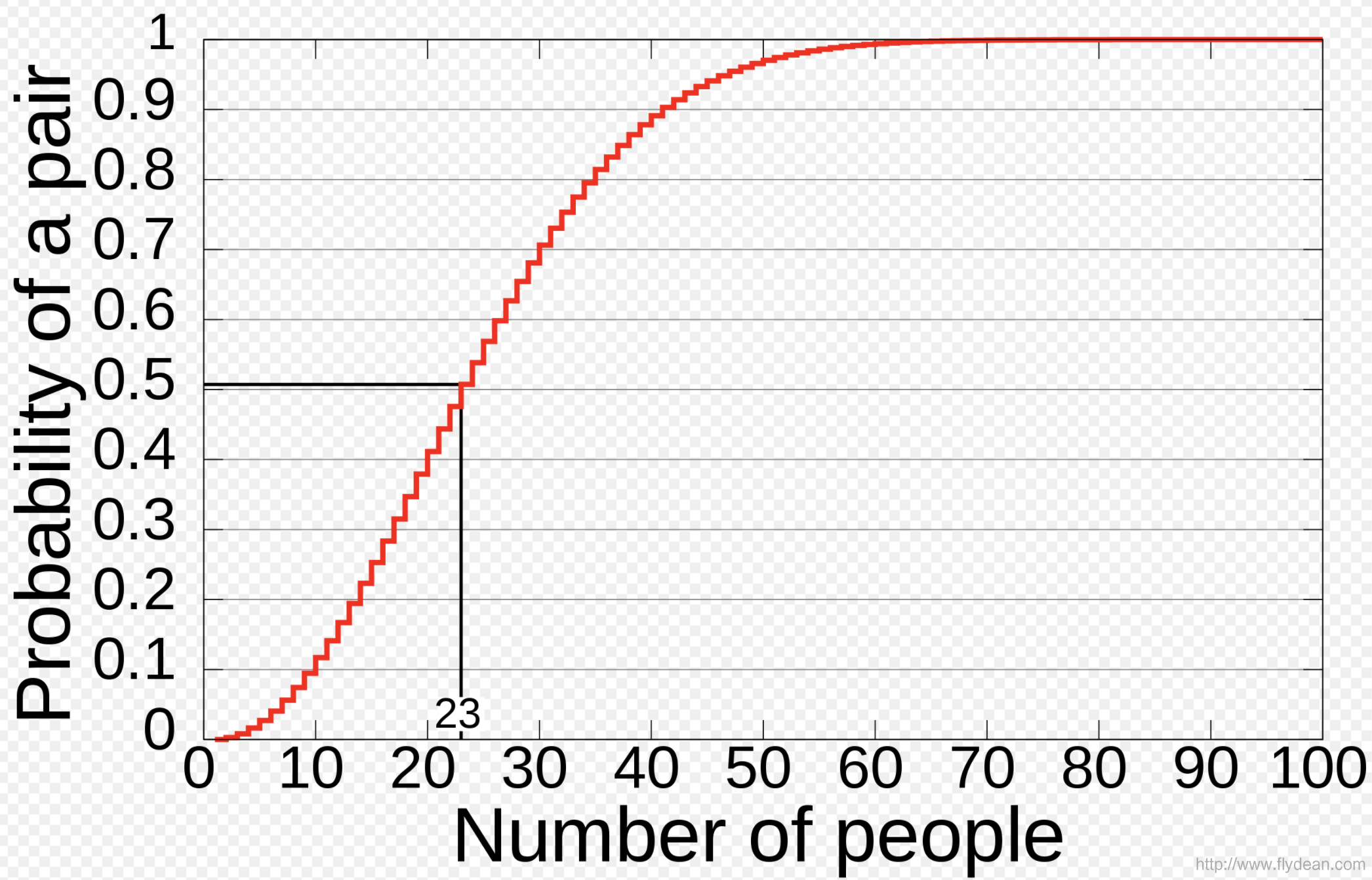
在实际应用中,可以应用生日问题中的概率模型,从而减少碰撞攻击的复杂度,或者来评估一个hash函数中可能出现碰撞攻击的几率。
怎么计算呢?
假如P(A) 是生日相同的概率,那么P(A) = 1 - P(A
一个人生日不同的概率是365/365,两个人生日不同的概率就是365/365 * 364/365 ,依次类推。
我们可以得到23个人生日不同的概率大概就是 0.492703。
也就是说23个人中有两个人生日相同的概率可以大于50%。
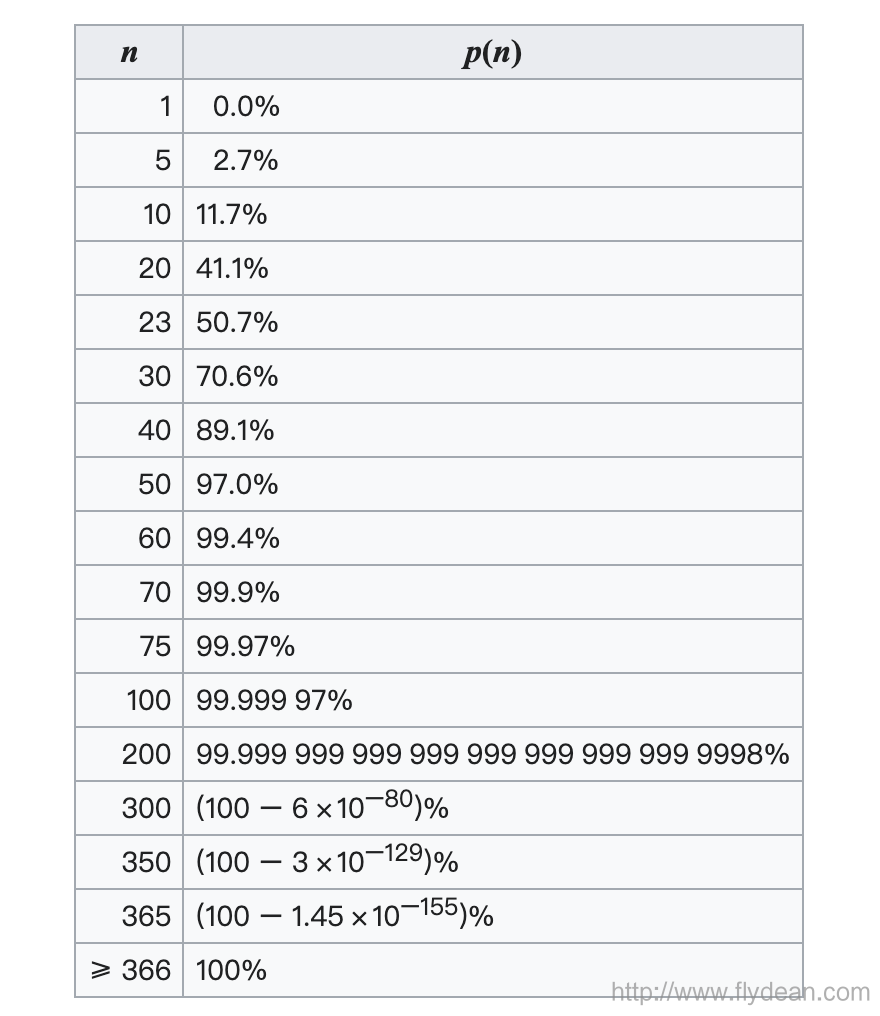
再看一张表来个更加直观的描述:
生日问题的衍生
生日问题的取值范围是在一年的365天之内,也就是说生日只可能有365种可能性。
我们将这个问题扩展一下到一般的情况,假设有一个函数f,它的输出范围是H,那么我们的攻击就是找到两个不同的x,y,让f(x)=f(y)。
这时候,我们可以称x和y发生了碰撞。
根据概率论的公式,我们想要达到50%的几率,那么需要尝试的次数是:
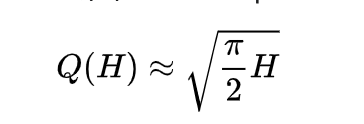
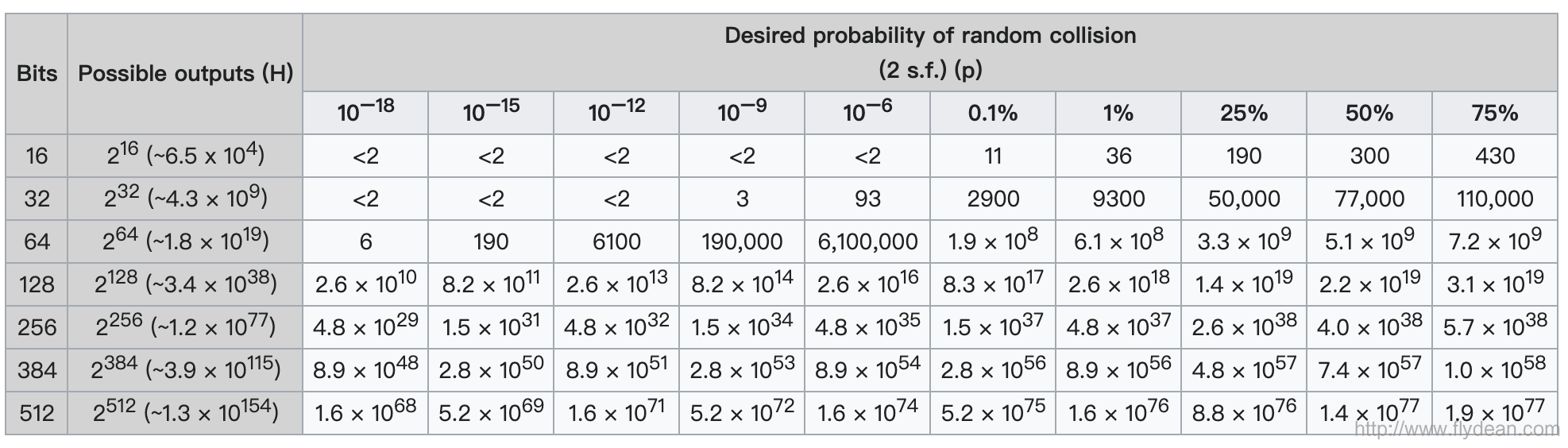
如果以bits位来表示可能计算出的结果的话,我们可以参考下面的概率表:
生日攻击的应用
生日攻击一般应用在数字签名中。一般来说为了对机密消息进行签名,因为加密的限制,如果消息很大的情况下,不可能对所有的消息进行签名,通常会对消息计算hash值,然后对这个hash值进行签名。
比如有人想做一个欺诈性的合同,那么会在原合同的基础上进行修改,不断的进行尝试,从而找到一个修改后的合同,让合同和之前合同的hash是一样的,从而导致两者的签名也是一样的。
怎么抵御这种攻击呢?根据我们生日攻击的公式,当然是将签名方案使用的哈希函数的输出长度选择得足够大,以使生日攻击在计算上变得不可行。
本文已收录于 http://www.flydean.com/birthday-attack/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!