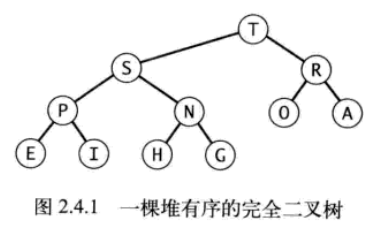
我们经常提到的数据结构大顶堆指的是二叉堆,它是一颗堆有序的完全二叉树(非叶子结点层都是满的,最后一层从右向左只能空缺右结点)。其中根节点是所有结点中最大,并且每个父节点都大于其两个子节点(堆有序)。完全二叉树底层是用数组实现的,所以它只是逻辑上的一个概念。下图是一个大顶堆的例子:
那么给定一个数组怎么建立大顶堆呢?我们用下面代码来说明,建立堆的时间复杂度为O(n)。
1 //建立大顶堆 2 public void creatHeap(int[] arr) { 3 for (int i=0; i<arr.length; i++) { 4 heapInsert(arr, i); 5 } 6 } 7 /** 8 * 某一个元素进堆,元素上浮的过程 9 * @param arr 10 * @param index 11 */ 12 public void heapInsert(int[] arr, int index) { 13 //当前元素大于父节点时,交换 14 while (arr[index] > arr[(index - 1) / 2]) { 15 swap(arr, index, (index - 1) / 2); 16 // 来到父节点位置继续比较 17 index = (index - 1) / 2; 18 } 19 } 20 21 public void swap(int[] arr, int m, int n) { 22 int temp = arr[m]; 23 arr[m] = arr[n]; 24 arr[n] = temp; 25 }
如果说堆中某个元素变小了,我们可以使用heapify来调整元素的位置,使得堆仍然是大顶堆,heapify实际上是当前元素下沉的过程,具体代码如下:
1 /** 2 * 元素下沉过程 3 * @param arr 4 * @param index 当前变小的元素 5 * @param heapSize 堆的大小,小于等于数组的大小 6 */ 7 public void heapify(int[] arr, int index, int heapSize) { 8 //左右孩子结点的索引,数组的索引从0开始 9 int left = 2 * index + 1; 10 int right = left + 1; 11 12 while (left < heapSize) { 13 //从左右孩子中选出大的 14 int largest = right < heapSize && arr[right] > arr[left] ? right : left; 15 //和index比较 16 largest = arr[largest] > arr[index] ? largest : index; 17 //当前变小的元素任然比左右孩子结点大,结束循环 18 if (largest == index) break; 19 //交换 20 swap(arr, largest, index); 21 //更新index位置,来到largest的位置 22 index = largest; 23 //重置left位置,继续向下比较 24 left = 2 * index + 1; 25 } 26 }
优先队列本质还是一个队列,只不过队列里的元素有优先级,优先级高的元素先出队列。在Java中优先队列有两种实现,一种是大顶堆,另外一种是小顶堆。以大顶堆为例:当队首元素弹出时,优先队列会自动调整剩下的元素,使其仍是一个大顶堆,时间复杂度为O(nlogn)。具体实现过程就利用了我们上面的heapify方法,同样给出代码说明:
1 public void heapSort(int[] arr) { 2 int len = arr.length; 3 //交换首尾元素,使得弹出的元素在堆中失效,但仍在数组中 4 swap(arr, 0, --len); 5 //不断地进行heapify操作 6 while (len > 0) { 7 heapify(arr, 0, len); 8 swap(arr, 0, --len); 9 } 10 }
优先队列可以应用于系统的任务调度,优先级高的任务先执行,低的在队列中等候;图的搜索算法中也会用到优先队列,感兴趣的童鞋可以阅读《算法》第四版具体学习。
参考资料:左程云算法初级班
《算法》第四版