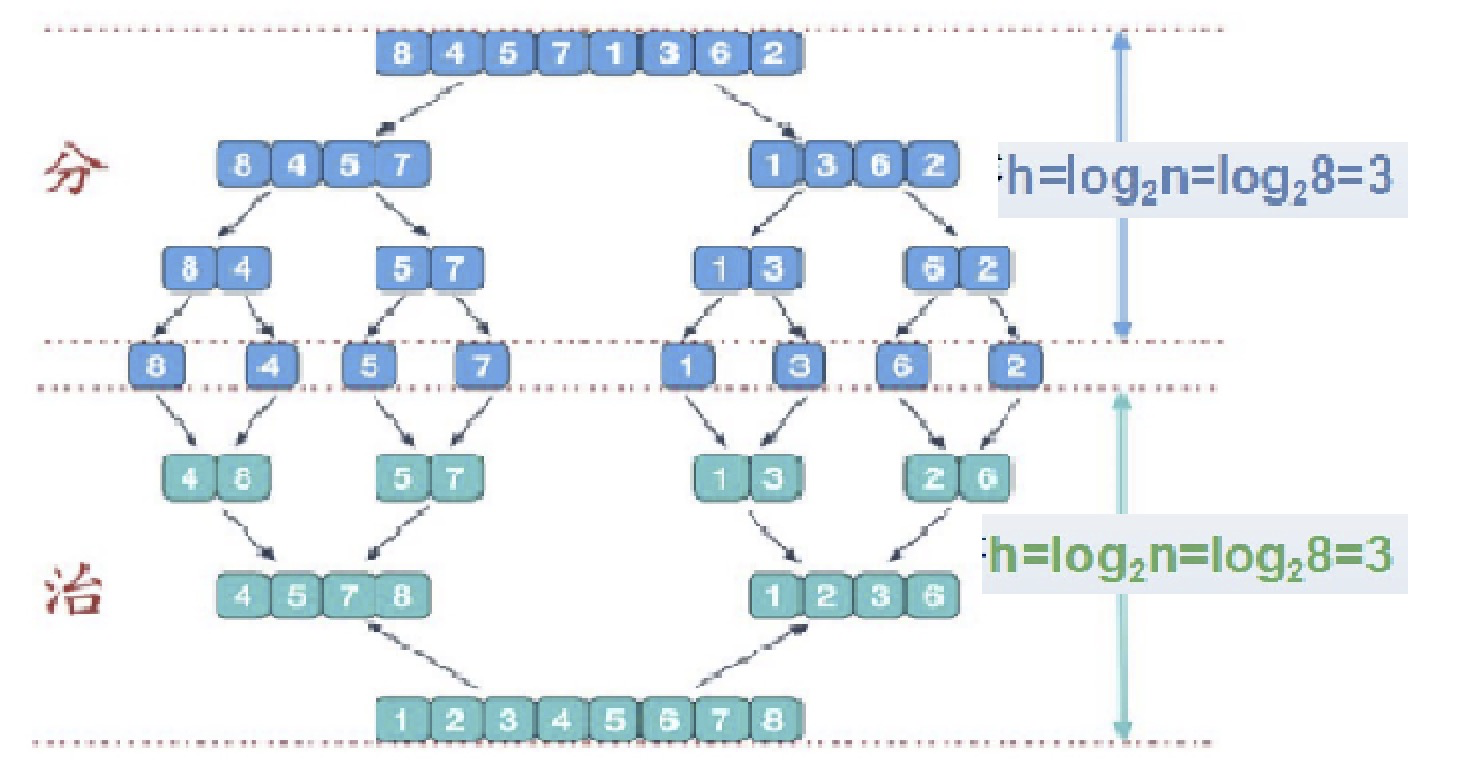
分阶段可以理解为就是递归拆分子序列的过程
治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8]
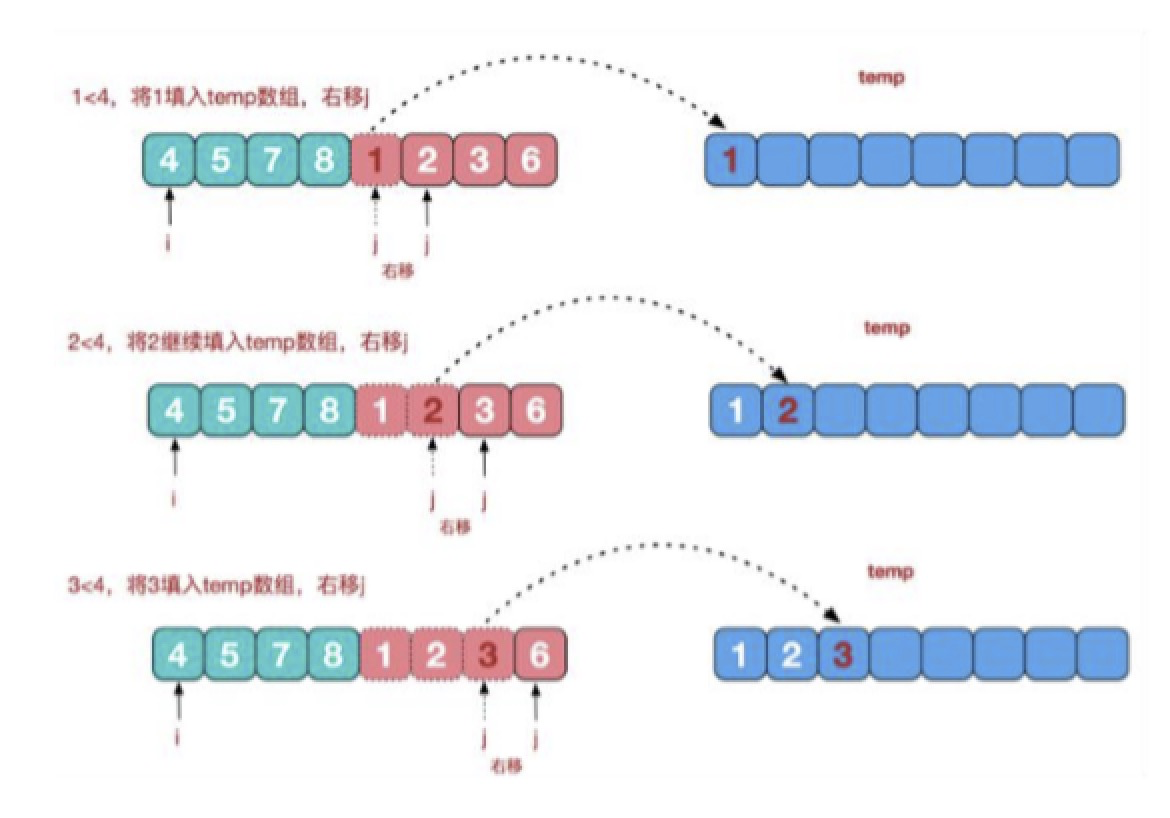

import java.util.Arrays; /** * 归并排序 */ public class MergeSort { public static void mergeSort(int[] arr,int left,int right,int[] temp){ if (left<right){ int mid = (left+right)/2; //前一部分分解 mergeSort(arr,left,mid,temp); //后一部分分解 mergeSort(arr,mid+1,right,temp); //合并 merge(arr,left,mid,right,temp); } } /** * 合并 如 4,5,7,8, 1,2,3,6 * @param arr 原始数组 由两部分组成 * @param left 数组的第一个索引 * @param mid 数组前一部分最后一个元素的索引 * @param right 数组的最后一个索引 * @param temp 临时数组 */ public static void merge(int[] arr,int left,int mid,int right,int[] temp){ System.out.println("从"+left+"到"+right+"中间为"+arr[mid]+"原始数组"+Arrays.toString(arr)); int i = left; int j = mid+1; int t = 0; while (i<=mid&&j<=right){ if (arr[i]<=arr[j]){ temp[t] = arr[i]; i++; t++; }else { temp[t] = arr[j]; j++; t++; } } while (i<=mid){ temp[t]=arr[i]; i++; t++; } while (j<=right){ temp[t]=arr[j]; j++; t++; } //将temp数组的元素拷贝到arr t = 0; int tempLeft = left; while (tempLeft<=right){ arr[tempLeft]=temp[t]; t++; tempLeft++; } System.out.println("合并后"+Arrays.toString(arr)); } public static void main(String[] args){ //测试合并 int[] arr = new int[]{4,5,7,8,1,2,3,6}; int length = arr.length; merge(arr,0,(length-1)/2,length-1,new int[arr.length]); //从0到7中间为8原始数组[4, 5, 7, 8, 1, 2, 3, 6] //合并后[1, 2, 3, 4, 5, 6, 7, 8] int[] arr2 = new int[]{9,8,7,6,5,4,3,2,1}; mergeSort(arr2,0,arr2.length-1,new int[arr2.length]); //从0到1中间为9原始数组[9, 8, 7, 6, 5, 4, 3, 2, 1] //合并后[8, 9, 7, 6, 5, 4, 3, 2, 1] //从0到2中间为9原始数组[8, 9, 7, 6, 5, 4, 3, 2, 1] //合并后[7, 8, 9, 6, 5, 4, 3, 2, 1] //从3到4中间为6原始数组[7, 8, 9, 6, 5, 4, 3, 2, 1] //合并后[7, 8, 9, 5, 6, 4, 3, 2, 1] //从0到4中间为9原始数组[7, 8, 9, 5, 6, 4, 3, 2, 1] //合并后[5, 6, 7, 8, 9, 4, 3, 2, 1] //从5到6中间为4原始数组[5, 6, 7, 8, 9, 4, 3, 2, 1] //合并后[5, 6, 7, 8, 9, 3, 4, 2, 1] //从7到8中间为2原始数组[5, 6, 7, 8, 9, 3, 4, 2, 1] //合并后[5, 6, 7, 8, 9, 3, 4, 1, 2] //从5到8中间为4原始数组[5, 6, 7, 8, 9, 3, 4, 1, 2] //合并后[5, 6, 7, 8, 9, 1, 2, 3, 4] //从0到8中间为9原始数组[5, 6, 7, 8, 9, 1, 2, 3, 4] //合并后[1, 2, 3, 4, 5, 6, 7, 8, 9] } }