【LeetCode-回溯】N皇后

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

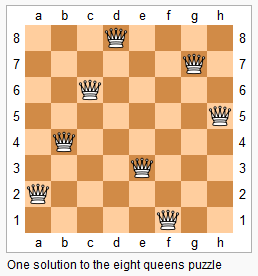
上图为 8 皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例：

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

题目链接： https://leetcode-cn.com/problems/n-queens/

思路

n皇后问题是经典的回溯算法问题。由于一行只能有一个皇后，所以不需要按位置迭代，只需要按行迭代即可。在每行找到合适的位置放置，然后放下一行；如果当前行找不到合适的位置，则回溯到上一行。合适的位置是指当前行、当前列以及当前皇后所在的两条对角线都没有皇后。
为了判断位置(row, col)是否是一个可以放置皇后的位置，我们使用一个长度为n的数组visit[n]，初始化数组元素为0，并设置visit[row]=col。例如，假设已经在(0,1)、(1,3)分别放置了两个皇后，则visit[0]=1, visit[1]=3。如果位置(row, col)满足下面3个条件中的一个，则说明(row, col)不能放置皇后：

• visit[i] == col; // 当前列已经有皇后了
• row+col == i+visit[i]; // 当前位置的主对角线上已经有皇后了
• row-col == i-visit[i]; // 当前位置的次对角线已经有皇后了

之所以没有判断当前行是否有皇后是因为我们每次都选择一个新行来放置皇后，所以不用判断。如果不满足这3个条件，则当前位置(row, col)可以放置皇后。代码如下：

class Solution {
public:
    vector<vector<string>> ans;
    vector<vector<string>> solveNQueens(int n) {
        if(n==0) return {{}};

        vector<vector<int>> board(n, vector<int>(n, 0));
        vector<int> visit(n, 0);
        int row = 0, col = 0;
        dfs(row, col, board, visit, n);
        return ans;
    }

    void dfs(int row, int col, vector<vector<int>> board, vector<int> visit, int n){    // col参数可以删除
        if(row==n){
            ans.push_back(transform(board));
            return;
        }

        for(int i=0; i<n; i++){ // 只对col进行循环
            if(isValid(row, i, visit)){
                board[row][i] = 1;
                visit[row] = i;
                dfs(row+1, i, board, visit, n);
                board[row][i] = 0;
                visit[row] = 0;
            }
        }
    }

    bool isValid(int row, int col, vector<int> visit){
        for(int i=0; i<row; i++){    // 注意这里是i<row，不是i<n
            if(visit[i]==col || row+col==i+visit[i] || row-col==i-visit[i]){
                return false;
            }
        }
        return true;
    }

    /*将01二维数组组成的棋盘转为'Q.'字符串组成的vector*/
    vector<string> transform(vector<vector<int>> board){
        vector<string> v;
        for(int i=0; i<board.size(); i++){
            string s = "";
            for(int j=0; j<board[i].size(); j++){
                if(board[i][j]==1) s+="Q";
                else s+=".";
            }
            v.push_back(s);
        }
        return v;
    }
};

也可以使用其他的方法来判断某一位置是否能放置皇后，如下（只对isValid函数进行了更改）：

class Solution {
public:
    vector<vector<string>> ans;
    vector<vector<string>> solveNQueens(int n) {
        if(n==0) return {{}};

        vector<vector<int>> board(n, vector<int>(n, 0));
        int row = 0, col = 0;
        dfs(row, col, board, n);
        return ans;
    }

    void dfs(int row, int col, vector<vector<int>> board, int n){
        if(row==n){
            ans.push_back(transform(board));
            return;
        }

        for(int i=0; i<n; i++){
            if(isValid(row, i, board)){
                board[row][i] = 1;
                dfs(row+1, i, board, n);
                board[row][i] = 0;
            }
        }
    }

    bool isValid(int row, int col, vector<vector<int>> board){
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 1) { // 同一列的上方元素
                return false;
            }
        }
        for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) { // 左上方斜对角线
            if (board[i][j] == 1) {
                return false;
            }
        }
        for (int i = row, j = col; i >= 0 && j < board.size(); i--, j++) { // 右上方斜对角线
            if (board[i][j] == 1) {
                return false;
            }
        }
        return true;
    }

    vector<string> transform(vector<vector<int>> board){
        vector<string> v;
        for(int i=0; i<board.size(); i++){
            string s = "";
            for(int j=0; j<board[i].size(); j++){
                if(board[i][j]==1) s+="Q";
                else s+=".";
            }
            v.push_back(s);
        }
        return v;
    }
};

这种方法没有使用visit数组的方法好记。