「POJ-3608」Bridge Across Islands （旋转卡壳--求两凸包距离）

题目链接 POJ-3608 Bridge Across Islands

题意

依次按逆时针方向给出凸包，在两个凸包小岛之间造桥，求最小距离。

题解

旋转卡壳的应用之一：求两凸包的最近距离。

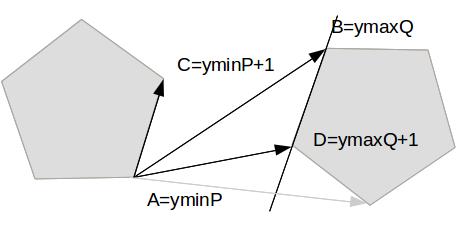
找到凸包 p 的 y 值最小点 yminP 和 q 的 y 值最大点ymaxQ，然后分别做切线如图。

那么(AC imes AD> AC imes AB)则说明B还不是离AC最近的点，所以++ymaxQ。

否则用 (AC) 和 (BD) 两个线段的距离更新最近距离，并且++yminP，即考察P的下一条边。

代码

#include <cstdio>
#include <cmath>
#include <algorithm>
#define sqr(x) (x)*(x)
#define N 50001
#define EPS (1e-8)
#define PI acos(-1.0)
#define INF (1e99)
using namespace std;
int sgn(double x) {
    if(fabs(x) < EPS)return 0;
	return (x < 0)?-1:1;
}
struct Point {
    double x,y;
    Point(double _x=0,double _y=0):x(_x), y(_y){}
    Point operator -(const Point &b)const {
        return Point(x - b.x,y - b.y);
    }
    Point operator +(const Point &b)const {
        return Point(x + b.x,y + b.y);
    }
    double operator ^(const Point &b)const {
        return x*b.y - y*b.x;
    }
    double operator *(const Point &b)const {
        return x*b.x + y*b.y;
    }
    void in(){
        scanf("%lf%lf",&x,&y);
    }
};
double dis2(Point a,Point b){
	return sqr(a-b);
}
double dist(Point a,Point b){
	return sqrt(dis2(a,b));
}
struct Line {
    Point s,e;
  	Line(){}
    Line(Point _s,Point _e):s(_s),e(_e) {}
};
double xmult(Point a,Point b,Point o){
    return (a-o)^(b-o);
}
double mult(Point a, Point b, Point o){
	return (a-o)*(b-o);
}
double disToSeg(Point P,Line L){
  if(!sgn(dis2(L.s,L.e)))
  	return dist(L.s,P);
  if(sgn(mult(P,L.e,L.s))<0)return dist(L.s,P);
  if(sgn(mult(P,L.s,L.e))<0)return dist(L.e,P);
  return fabs(xmult(P,L.s,L.e))/dist(L.s,L.e);
}
double segToSeg(Line l1,Line l2){
    return min(min(disToSeg(l1.s,l2),disToSeg(l1.e,l2)),min(disToSeg(l2.s,l1),disToSeg(l2.e,l1)));
}
Point p[N],q[N];
int n,m;
double qiake(){
    int yminp=0,ymaxq=0;
    for(int i=1;i<n;++i)
        if(p[i].y<p[yminp].y)
            yminp=i;
    for(int i=1;i<m;++i)
        if(q[i].y>q[ymaxq].y)
            ymaxq=i;
    p[n]=p[0];
    q[m]=q[0];
    double tmp,ans=INF;
    for(int i=0;i<n;++i){
        while(tmp=sgn(xmult(p[yminp+1],q[ymaxq+1],p[yminp])
        -xmult(p[yminp+1],q[ymaxq],p[yminp]))>0)
            ymaxq=(ymaxq+1)%m;
        ans=min(ans,segToSeg(Line(p[yminp],p[yminp+1]),Line(q[ymaxq],q[ymaxq+1])));
        yminp=(yminp+1)%n;
    }
    return ans;
}
int main(){
    while(~scanf("%d%d",&n,&m)&&n&&m){
        for(int i=0;i<n;++i)
            p[i].in();
        for(int i=0;i<m;++i)
            q[i].in();
        printf("%f
",qiake());
    }
    return 0;
}