一 综述
线段树是一种类似与二叉搜索树的结构,及非叶子节点一定包含了左右子树。每个节点存储了一个区间(线段)的值(可以是最值,区间和等)。所以对于这个节点,需要的信息应该包括
该节点表示的连续区间l,以及该节点的数据。
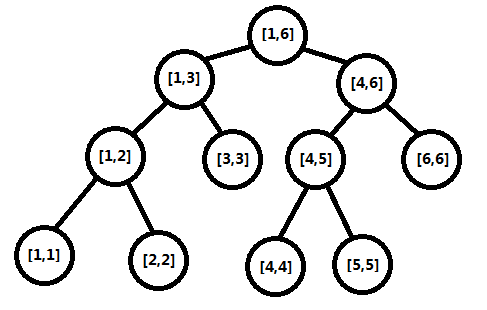
我们可以用线段树来做什么呢?线段树可以在log(n)的时间内实现区间修改(单点修改)和区间查询。其操作的原理就是我们将区间表示成几个连续的小区间,通过对这几个连续小区间的操作
实现对我们想要操作节点的操作。(可以证明一定可以由log(n)*2个区间来表示)
二 线段树的常用操作
定义
#define maxn 100007 int sum[maxn<<2],add[maxn<<2]; //sum表示区间和,add是懒惰标记 int a[maxn],n;//a数组存储原数据 下标1-n
建树
void build(int p,int l,int r) { if(l==r) //递归到了叶子节点 { sum[p]=a[l]; return; } int m=(l+r)>>1; //递归左右子树 build(p<<1,l,mid); build(p<<1|1,mid+1,r); PushUp(p); }
维护区间和
void PushUp(int rt) { sum[rt]=sum[rt<<1]+sum[rt<<1|1]; }
单点更新: 将某个节点的值进行更新。则从该节点到根节点的路径上的节点都需要更新
void update(int L,int C,int l,int r,int p) //L是要更新的结点,C是值,p是当前的节点 { if(l==r) { sum[p]+=C; return; } int m=(l+r)>>1; //根据L判断更新左还是右子树 if(L<=m) update(L,C,l,m,p<<1); else update(L,C,m+1,r,p<<1|1); PushUp(p); }
区间更新
说下add数组的意义。用来标记本节点已经更新过了,但是本节点的子节点并没有更新,所以需要进行下推操作
下推操作:
void PushDown(int ln,int rn,int p)//ln,rn表示左右子树的数字数量 { if(add[p]) { add[p<<1]+=add[p]; add[p<<1|1]+=add[p]; //修改子节点的sum使之与对应的add相对应 sum[p<<1]+=add[p<<1]*ln; sum[p<<1|1]+=add[p<<1|1]*rn; //清除本节点标记 add[rt]=0; } }
区间更新
void update(int L,int R,int C,int l,int r,int p) //L,R为要更新的区间,C是值 { if(L<=l&&r<=R) //如果当前区间完全在要更新的区间中 { sum[p]+=C*(r-l+1);//更新数字和,向上保持正确 add[p]+=C; //增加add标记,表示本区间的sum正确,子区间的sum仍然需要更新 return; } int m=(l+r)>>1; PushDown(p,m-l+1,r-m); //下推标记 //判断左右子树和[L,R]有无交集,有交集才能递归 if(L<=m) update(L,R,C,l,m,p<<1); else update(L,R,C,m+1,r,p<<1|1); PushUp(p); //更新本节点 }
区间查询:
int query(int L,int R,int l,int r,int p) { if(L<=l&&r<=R) return sum[p]; int m=(l+r)>>1; //下推标记,否则sum可能不正确 PushDown(p,m-l+1,r-m); int ans=0; if(L<=m) ans+=query(L,R,l,m,p<<1); else ans+=query(L,R,m+1,r,p<<1|1); return ans; }
三 应用之扫描线
用结构体存储矩形的x1,x2,y,flag(顶边或者底边),X数组存储所有的x下标值,Line记录所有的矩形定边和底边信息。将X和Line排序
遍历Line,从最小的y值开始访问,找到对应x1,x2在X数组的下标值。用线段树维护矩形的变成,cover来代表点是否被覆盖(每出现一条顶边,要相应删除一条底边)
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int maxn=10010; int sum[maxn<<2],cover[maxn<<2];//sum来维护某个区间的,cover表示是否覆盖 int X[maxn]; //存储所有的x下标值 struct Line { int lx,rx,y; int flag; Line(){} Line(int a,int b,int c,int d) { lx=a;rx=b; y=c;flag=d; } bool operator <(const Line&B) { return y<B.y; } }line[maxn]; int find(int key,int n) { int low=1,high=n,mid; while(low<=high) { mid=(low+high)>>1; if(X[mid]==key) return mid; else if(X[mid]<key) low=mid+1; else high=mid-1; } return -1; } void PushUp(int u,int l,int r) //维护矩形的长 { if(cover[u]) { sum[u]=X[r+1]-X[l]; } else if(l==r) sum[u]=0; else { sum[u]=sum[u<<1]+sum[u<<1|1]; } } void update(int p,int l,int r,int L,int R,int flag) { if(L<=l&&r<=R) { cover[p]+=flag; PushUp(p,l,r); return; } int m=(l+r)>>1; if(L<=m) update(p<<1,l,m,L,R,flag); if(R>m) update(p<<l|1,m+1,r,L,R,flag); /*if(R<=m) update(p<<1,l,m,L,R,flag); else if(L>m) update(p<<1|1,m+1,r,L,R,flag); else { update(p<<1,l,m,L,m,flag); update(p<<1|1,m+1,r,m+1,R,flag); } PushUp(p,l,r);*/ } int main() { int n,x1,y1,x2,y2; scanf("%d",&n); int num=0; for(int i=1;i<=n;i++) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); X[++num]=x1; line[num]=Line(x1,x2,y1,1); X[++num]=x2; line[num]=Line(x1,x2,y2,-1); } sort(X+1,X+1+num); sort(line+1,line+1+num); int k=1; for(int i=2;i<=num;i++) if(X[i]!=X[i-1]) X[++k]=X[i]; int ans=0; for(int i=1;i<=num;i++) { //找到扫描线左右端点在X数组中的下标 int l=find(line[i].lx,k); int r=find(line[i].rx,k)-1; //为什么要-1 if(l<=r) update(1,1,k,l,r,line[i].flag); for(int i=1;i<=20;i++) cout<<cover[i]<<" "; cout<<endl; ans+=sum[1]*(line[i+1].y-line[i].y); } printf("%d ",ans); }