曼哈顿距离 Manhattan Distance
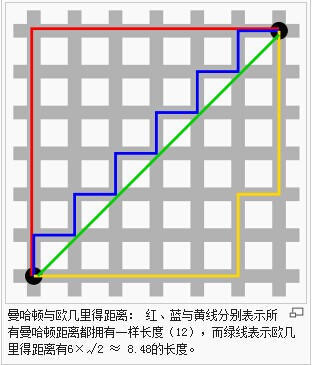
由来:
曼哈顿距离 Manhattan Distance,又被称为出租车距离,是因为在像纽约曼哈顿区这样的地区,有很多由横平竖直的 街道 所切成的 街区(Block)。
出租车司机计算从一个位置到另一个位置的距离,通常直接用街区的两个坐标分别相减,再相加,这个结果就是他即将开车通过的街区数量。
计算公式:
以二维平面为例,假设有两个点 i ((x_1, y_1)) 和 点 j ((x_2, y_2)),他们的距离为:
$ d(i, j) = |x_2 - x_1| + |y_2 - y_1|$
特性:
- 值一定非负,最小为0,即两点重合的情况。
欧氏距离
欧拉距离
在二维空间中 点a 和 点b 的距离
(sqrt{(x^{(a)} - x^{(b)})^2 + (y^{(a)} - y^{(b)})^2})
在三维空间中 点a 和 点b 的距离
(sqrt{ (x^{(a)} - x^{(b)})^2 + (y^{(a)} - y^{(b)})^2+ (z^{(a)} - z^{(b)})^2 })
扩展到 n 维空间,使用x,y,z 这样的字母不方便,所以使用以下字母表示:
X:整个数据
(X^{(a)}):第 a 个数据
(X^{(b)}):第 b 个数据
计算a,b 两个样本之间的距离
(sqrt{ (X_1^{(a)} - X_1^{(b)})^2 + (X_2^{(a)} - X_2^{(b)})^2+ ... + (X_n^{(a)} - X_n^{(b)})^2 })
也可记为:
(sqrt{ sum^n_{i=1} (X_i^{(a)} - X_i^{(b)})^2 })
从 i=1 开始对 a 样本的第 i 个特征 和 b 样本的第i个特征相减、平方、相加、开根号。
闵可夫斯基距离 Minkowski Distance
欧式距离也可记为:
$ (sum^n_{i=1} |X_i^{(a)} - X_i{(b)}|2)^{frac{1}{2}} $
曼哈顿距离可记为:
$ (sum^n_{i=1} |X_i^{(a)} - X_i{(b)}|){frac{1}{1}} $
以上两种距离在数学形式上具有一致性,推而广之可得到 闵可夫斯基距离:
$ (sum^n_{i=1} |X_i^{(a)} - X_i{(b)}|p)^{frac{1}{p}} $
p 称为范式;
p = 1:曼哈顿距离,p = 2:欧氏距离;
再进一步泛化,可得:
$||x||p = (sum{I=1}^p |x_i|^p )^{frac{1}{p}} $
切比雪夫距离 Chebyshev distance
各坐标数值差的最大值
$ dis=max( |x1-x2|, |y1-y2|) $
汉明距离 Hamming distance
将一个字符串变换成另外一个字符串所需要替换的字符个数
1011101 与 1001001 之间的汉明距离是 2。
2143896 与 2233796 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
向量空间余弦相似度 Cosine Similarity
夹角余弦
设向量a和向量b,则a•b=|a||b|cos ,
|a|和|b|分别为两向量的模
cos 即为两向量的余弦值,
所以 (cos = frac{a•b}{|a||b| })
https://www.cnblogs.com/renpfly/p/9553910.html