【第1章 绪论】
学习算法:机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”的算法,即“学习算法”。
学习算法的作用:1.基于提供的经验数据产生模型;
2.面对新情况时,模型可提供相应的判断。
模型:泛指从数据中学得的结果。
学习器:学习算法在给定数据和参数空间上的实例化。

要进行机器学习,先要有数据。
数据集:一组记录的集合。
示例/样本/特征向量:每条记录(关于一个事件或对象的描述)或空间中的每一个点(对应一个坐标向量)。
属性/特征:反应事件或对象在某方面的表现或性质的事项。
属性值:属性上的取值。
属性空间/样本空间/输入空间:属性张成的空间。
维数:属性的个数。
模型需要从数据中学得。
学习/训练:从数据中学得模型的过程。
训练数据:训练过程中使用的数据。
训练样本:每个样本。
训练集:训练样本组成的集合。
假设:学习模型对应了关于数据的某种潜在的规律。
真相/真实:这种潜在规律自身。
学习过程就是为了找出或逼近真相。
获得训练样本的结果信息,才能建立“预测”的模型。
标记:关于示例结果的信息。
样例:拥有了标记信息的示例。
标记空间:所有标记的集合。
测试:学得模型后,使用其进行预测的过程。
测试样本:被预测的样本。
聚类:将训练集中的训练样本分成若干组。
簇:每组称为一个“簇”,这些自动形成的“簇”可能对应一些潜在的概念划分。
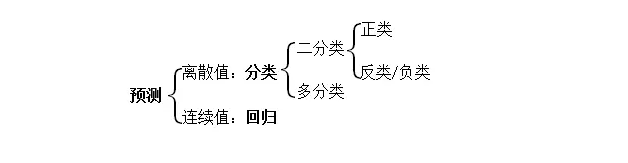
根据训练数据是否拥有标记信息,学习任务可大致划分为两类。

机器学习的目标是使学得的模型能更好地适用于“新样本”。
泛化:学得模型适用于新样本的能力。

学习过程看作一个在所有假设组成的空间中进行的搜索的过程,搜索目标是找到与训练集“匹配”的假设。
假设空间:机器学习中可能的函数构成的空间称为“假设空间”。
版本空间:一个与训练集一致的“假设集合”。
归纳偏好:机器学习算法在学习过程中对某种类型假设的偏好。
任何一个有效的机器学习算法必有其归纳偏好。
“奥卡姆剃刀”原则:“若有多个假设与观察一致,则选最简单的那个。”
注意: 奥卡姆剃刀并非唯一可行的原则;
奥克姆剃刀本身存在不同的诠释。
“没有免费的午餐”定理(NFL定理):总误差与学习算法无关。
注意: 脱离具体问题,空泛的谈论“什么学习算法更好”,毫无意义。
P5 假设空间的规模问题
1. 某一属性值无论取什么都合适,我们用通配符“*”来表示。
2. 世界上没有,我们用“∅”来表示。
书中例子为西瓜,为判断西瓜的好坏,其属性有三种,即:色泽、根蒂、敲声。
这三种属性分别有3、3、3种可能取值,但假设空间的规模却是4×4×4+1=65。
这是因为,在假设空间中,属性的“无论取什么属性值都合适”也是一种属性值,而不是作为单一属性的3种可能取值的集合存在。
因为假设空间是机器学习中可能的函数构成的空间,“无论取什么属性值都合适”意味着这个函数与这一属性无关。
例如,如果西瓜的三个属性取值都是“无论取什么属性值都合适”,那么无论什么瓜,都是好瓜。而不是3×3×3=27个种类的瓜的集合,并不需要依次判断,需要的判断仅仅是——它是瓜。
所以其假设空间为:
{青绿,乌黑,浅白,*}×{蜷缩,稍蜷,硬挺,*}×{浊响,清脆,沉闷,*}+1(没有“好瓜”的定义)=65
1.1 表1.1中若只包含编号为1和4的两个样例,试给出相应的版本空间。
解:

如表1.1所示,好瓜和非好瓜的三个属性的属性值均不相同,故与训练集一致的假设集合即版本空间如下图所示:
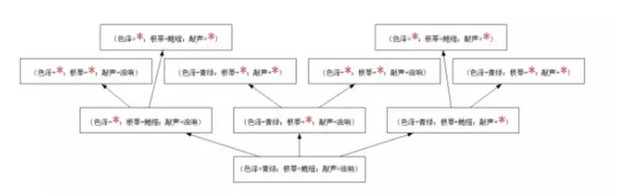
图1.1 版本空间
其取值则共有七种,其合取式为:
(色泽=青绿)∧(根蒂= ∗ )∧(敲声= ∗ )
(色泽= ∗ )∧(根蒂=蜷缩)∧(敲声= ∗ )
(色泽= ∗ )∧(根蒂= ∗ )∧(敲声=浊响)
(色泽=青绿)∧(根蒂=蜷缩)∧(敲声= ∗ )
(色泽=青绿)∧(根蒂= ∗ )∧(敲声=浊响)
(色泽= ∗ )∧(根蒂=蜷缩)∧(敲声=浊响)
(色泽=青绿)∧(根蒂=蜷缩)∧(敲声=浊响)
1.2 与使用单个合取式来进行假设表示相比,使用“析合范式”将使得假设空间具有更强的表示能力。例如:
好瓜←→((色泽=*)∧(根蒂=蜷缩)∧(敲声=*))∨((色泽=乌黑)∧(根蒂=*)∧(敲声=沉闷))
会把“((色泽=青绿)∧(根蒂=蜷缩)∧(敲声=清脆))”以及“((色泽=乌黑)∧(根蒂=硬挺)∧(敲声=沉闷))”都分类为“好瓜”。
若使用最多包含k个合取式的析合范式来表达表1.1西瓜分类问题的假设空间,试估算共有多少种可能的假设。
解:

计算此题,先要计算假设空间的规模,之前笔者一直被P5 中三种属性的3种属性值迷惑,以为此表也应如此计算。
但实际上,此表的色泽属性只有:1.青绿、2.乌黑 两种属性值,故其规模大小为: 3×4×4+1=49种。
k的最大值为49。
使用最多包含k个合取式的析合范式有如下多种可能:
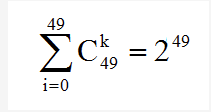
p.s.很多博主都分别讨论了是否存在冗余的两种情况,笔者则认为冗余由于分析的步骤不同而不存在。
1.3 若数据包含噪声,则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下,试设计一种归纳偏好用于假设选择。
解:
归纳偏好:在训练过程中选择满足最多样本的假设。
1.4 本章1.4节在论述“没有免费的午餐”定理时,默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量l,试证明没有免费的午餐”定理仍成立。
解:
考虑二分类问题,NFL首先要保证真是目标函数f均匀分布,对于有X个样本的二分类问题,显然f共有2X种情况。其中一半是与假设一致的,也就 P(f(x)=h(x))=0.5。 此时, ∑fl(h(x),f(x))=0.5∗2X∗(l(h(x)=f(x))+l(h(x)≠f(x))) l(h(x)=f(x))+l(h(x)≠f(x))应该是个常数,隐含的条件就该是(一个比较合理的充分条件) l(0,0)=l(1,1),l(1,0)=l(0,1)。如果不满足, NFL 应该就不成立了(或者不那么容易证明)。