由素数筛法到欧拉函数（欧拉函数，线性筛）

前言

蒟蒻最近准备狂补数学啦TAT

基于筛素数，可以同时快速求出欧拉函数。于是蒟蒻准备从这里入手，整理一下实现的思路。

筛素数及其一种改进写法

传统筛素数的做法（埃式筛）是，利用已知的素数，去筛掉含有此质因子的合数，十分巧妙。由于不是本文的重点，就只贴一下代码吧

#include<cstdio>
#include<cmath>
#define R register int
const int N=100000000,SQ=sqrt(N);
bool f[N];
int main(){
	R i,j;
	for(i=2;i<=SQ;++i){
		if(f[i])continue;
		for(j=i<<1;j<N;j+=i)f[j]=1;
	}
	/*for(i=2;i<N;++i)
		if(!f[i])printf("%d
",i);*/
	return 0;
}

复杂度不会证，不过较近似于线性（大概是(O(nloglog n))的样子）。

实际上蒟蒻打了个表，N与筛的次数大概有这样的关系

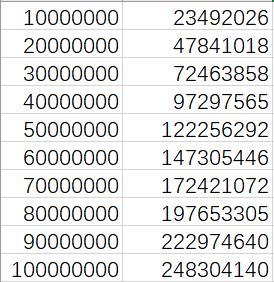
为什么是近似的呢？因为每个合数会被其多个质因子都筛一遍，所以并不是严格的。

于是我们要想办法让每个合数只被筛掉一次。如何实现呢？我们可以让每个合数都只被其最小质因子筛掉（欧拉筛）。

与上面相比，这种新的更加优秀的写法有了较大的变化。代码如下，可结合注释理解，也不多讨论。

#include<cstdio>
#include<cmath>
#define R register int
const int N=100000000,B=N>>1;
bool f[N];
int pr[B];
int main(){
	R i,j,p=0;
	for(i=2;i<=B;++i){
		if(f[i])
			for(j=1;j<=p&&i*pr[j]<N;++j){
				f[i*pr[j]]=1;
				if(!(i%pr[j]))break;//这一句话就是使得每个合数只被最小质因子筛掉的关键
//简要解释一下，如果pr[j]|i，那么i就有一个质因子pr[j]
//那么{i*pr[j+k],k∈N*}的最小质因子就是pr[j]而不是pr[j+k]了
			}
		else{
			pr[++p]=i;
			for(j=1;j<=p&&i*pr[j]<N;++j)
				f[i*pr[j]]=1;//i是质数，所以可以省掉上面那个判断，减小常数
		}
	}
	/*for(i=2;i<N;++i)
		if(!f[i])printf("%d
",i);*/
	return 0;
}

实际运行(N=10^8)比上面那种写法快一半。

欧拉函数

定义及性质

对一个正整数(x)定义欧拉函数(phi(x))，为([1,x])中与(x)互质的整数个数。

几个基本内容（下面定义(p)为质数）：

1. (phi(1)=1)，这个没啥好说的，因为本来就定义(1)与(1)互质
2. (phi(p)=p-1)，也是很显然的，由质数定义得出
3. 如果(p|x)，那么(phi(x*p)=phi(x)*p)，否则(phi(x*p)=phi(x)*（p-1))。证明的话百度一下吧，蒟蒻不会qwq

这样的话，是不是可以像埃式筛一样，通过某个质数筛去质因子含这个数的合数的同时，计算出这个合数的欧拉函数值呢？好像是不行的，因为可能两个数的商的欧拉函数值还没求出来。

这时候，更好的欧拉筛又派上了用场。枚举(x)再枚举质数(p)，这时候(phi(x))和(phi(p))肯定都求出来啦，那么(phi(x*p))当然也就求出来啦。

#include<cstdio>
#define R register
const int N=1000001;
int pr[N],phi[N];
bool f[N];
int main(){
	R int n,i,j,k,p=0;
	phi[1]=1;//内容1
	for(i=2;i<N;++i){
		if(!f[i])phi[pr[++p]=i]=i-1;//内容2
		for(j=1;j<=p&&(k=i*pr[j])<N;++j){
			f[k]=1;
			if(i%pr[j])//内容3
				phi[k]=phi[i]*(pr[j]-1);
			else{
				phi[k]=phi[i]*pr[j];
				break;
			}
		}
	}
	return 0;
}

题目

一道模板题及其Sol