P2787 语文1（chin1）- 理理思维

题目背景

蒟蒻HansBug在语文考场上，挠了无数次的头，可脑子里还是一片空白。

题目描述

考试开始了，可是蒟蒻HansBug脑中还是一片空白。哦不！准确的说是乱七八糟的。现在首要任务就是帮蒟蒻HansBug理理思维。假设HansBug的思维是一长串字符串（字符串中包含且仅包含26个字母），现在的你，有一张神奇的药方，上面依次包含了三种操作：

1. 获取第x到第y个字符中字母k出现了多少次

2. 将第x到第y个字符全部赋值为字母k

3. 将第x到第y个字符按照A-Z的顺序排序

你欣喜若狂之时，可是他脑细胞和RP已经因为之前过度紧张消耗殆尽，眼看试卷最后还有一篇800字的作文呢，所以这个关键的任务就交给你啦！

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示HansBug的思维所包含的字母个数和药方上操作个数。

第二行包含一个长度为N的字符串，表示HansBug的思维。

第3-M+2行每行包含一条操作，三种操作格式如下：

1. 操作1： 1 xi yi ki 表示将第xi到第yi个字符中ki出现的次数输出

2. 操作2： 2 xi yi ki 表示将第xi到第yi个字符全部替换为ki

3. 操作3： 3 xi yi 表示将第xi到第yi个字符按照A-Z的顺序排序

输出格式：

输出为若干行，每行包含一个整数，依次为所有操作1所得的结果。

输入输出样例

输入样例#1： 

10 5
ABCDABCDCD
1 1 3 A
3 1 5
1 1 3 A
2 1 2 B
1 2 3 B

输出样例#1： 

1
2
2

说明

样例说明：

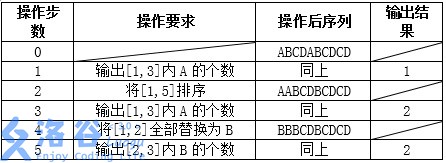
数据规模：

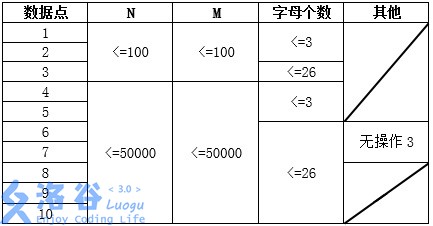
此题目中大小写不敏感。

Solution：

　　本题线段树的做法实在是巧妙～～。

　　理理思维，因为只有$26$个字母（忽略大小写后），于是我们将每个字母映射为$0$到$25$的数字，可以建$26$棵线段树来维护每个数字出现的个数（注意，千万不要写数组般的线段树，不好进行第三个操作，所以最好用结构体来存。记得对结构体中成员清$0$！由于这个我调了很久～）

　　讲下向上维护时的$pushup$，我们这里骚操作重载运算符$+$，将其定义为将两个结构体变量的成员$p[]$（即维护的$26$棵线段树）累加，返回一个结构体变量，这波操作能方便后面的$query$。那么$pushup$就是将当前左右儿子的信息累加到当前节点就好了。

　　然后我们考虑区间修改$update$操作，正常的判断区间包含然后直接修改，这里设置懒惰标记（初值为$-1$）,每次修改后就标记，然后下放时就将左右儿子维护的数组清$0$，赋值为当前的数字所对应的长度。

　　重点的查询，我们直接返回维护当前查询区间的结构体变量，这样对于操作$1$，直接输出某个$p[i]$的值即可，而对于操作$3$直接从前往后扫模拟一遍，暴力成段修改，最多也就$26$次$update$。

　　那么本题就$OK$了。

代码：

#include<bits/stdc++.h>
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define il inline
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Max(a,b) ((a)>(b)?(a):(b))
using namespace std;
const int N=50005;
int n,m,ss[N],lazy[N<<2];
char s[N];
struct node{
    int p[28];
    void cler(){memset(p,0,sizeof(p));}
}t[N<<2],emp;
node operator + (node a,node b){
    node c;
    For(i,0,25)c.p[i]=a.p[i]+b.p[i];
    return c;
}
il int gi(){
    int a=0;char x=getchar();
    while(x<'0'||x>'9')x=getchar();
    while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
    return a;
}
il int change(char x){return (x>='a'&&x<='z')?x-'a':x-'A';}
il void pushup(int rt){For(i,0,25)t[rt].p[i]=t[rt<<1].p[i]+t[rt<<1|1].p[i];}
il void pushdown(int rt,int len){
    if(lazy[rt]!=-1){
        lazy[rt<<1]=lazy[rt],lazy[rt<<1|1]=lazy[rt];
        t[rt<<1].cler();t[rt<<1|1].cler();
        t[rt<<1].p[lazy[rt<<1]]=(len-(len>>1)),t[rt<<1|1].p[lazy[rt<<1|1]]=(len>>1);
        lazy[rt]=-1;
    }
}
il void build(int l,int r,int rt){
    if(l==r){t[rt].cler();t[rt].p[change(s[l])]=1;return;}
    int m=l+r>>1;
    build(lson),build(rson);
    pushup(rt);    
}
il void update(int L,int R,int c,int l,int r,int rt){
    if(L<=l&&R>=r){
        t[rt].cler(),lazy[rt]=c;
        t[rt].p[c]=r-l+1;return;
    }
    int m=l+r>>1;
    pushdown(rt,r-l+1);
    if(L<=m)update(L,R,c,lson);
    if(R>m)update(L,R,c,rson);
    pushup(rt);
}
il node query(int L,int R,int l,int r,int rt){
    if(L<=l&&R>=r)return t[rt];
    node ret;
    ret.cler();
    int m=l+r>>1;
    pushdown(rt,r-l+1);
    if(L<=m)ret=ret+query(L,R,lson);
    if(R>m)ret=ret+query(L,R,rson);
    return ret;
}
int main(){
    n=gi(),m=gi();
    scanf("%s",s+1);
    memset(lazy,-1,sizeof(lazy));
    build(1,n,1);
    int f,x,y;char z[2];
    while(m--){
        f=gi();x=gi();y=gi();
        if(f!=3)scanf("%s",z);
        if(f==1) printf("%d
",query(x,y,1,n,1).p[change(z[0])]);
        else if(f==2) update(x,y,change(z[0]),1,n,1);
        else {
            node tmp=query(x,y,1,n,1);
            int l,r=x-1;
            For(i,0,25){
                if(!tmp.p[i])continue;
                l=r+1,r=l+tmp.p[i]-1;
                update(l,r,i,1,n,1);
            }
        }
    }
    return 0;
}