prim算法(解决修路问题)

prim算法(解决修路问题)

定义:

普利姆(Prim)算法求最小生成树，也就是在包含 n 个顶点的连通图中，找出只有(n-1)条边包含所有 n 个顶点的连通子图，也就是所谓的极小连通子图

关于最小生成树:

修路问题本质就是就是最小生成树问题， 先介绍一下最小生成树(Minimum Cost Spanning Tree)，简称 MST。给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树

1)   N 个顶点，一定有 N-1 条边

2)   包含全部顶点

3)   N-1 条边都在图中

4)   举例说明(如图:)

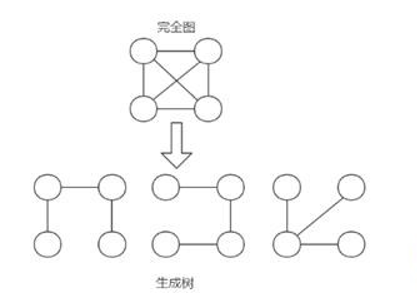
5)   求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法

问题:

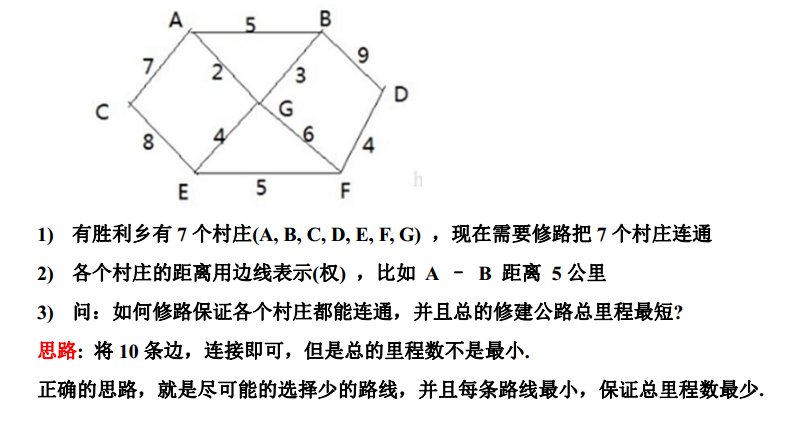
 思路分析：

 代码实现

package com.edu.algorithm.普利姆算法;

import java.util.ArrayList;
import java.util.List;

/**
 * <p>prim算法解决修路问题</p>
 *
 * @作者 five-five
 * @创建时间 2020/9/2
 */
public class 修路问题 {
    private static List<Character> characters = new ArrayList<>();
    public static void main(String[] args) {
        char[] chars = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};//表示顶点
        //只要权重不是不是Integer.MAX_VALUE，就说明个顶点连接的，而且数字表示两条路权重
        int[][] weight = new int[][]{
                //a                b c     d              e                 f                g
                {Integer.MAX_VALUE, 5, 7, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 2},//a
                {5, Integer.MAX_VALUE, Integer.MAX_VALUE, 9, Integer.MAX_VALUE, Integer.MAX_VALUE, 3},//b
                {7, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 8, Integer.MAX_VALUE, Integer.MAX_VALUE},//c
                {Integer.MAX_VALUE, 9, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, Integer.MAX_VALUE},//d
                {Integer.MAX_VALUE, Integer.MAX_VALUE, 8, Integer.MAX_VALUE, Integer.MAX_VALUE, 5, 4},//e
                {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, 5, Integer.MAX_VALUE, 6},//f
                {2, 3, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, 6, Integer.MAX_VALUE},};//g
        prim(weight, chars);
        System.out.println(characters);
    }

    private static void prim(int[][] weight, char[] chars) {
        prim(weight, chars, 0);
    }

    /**
     * @param weight
     * @param chars
     * @param start  从那个地方开始
     * @return
     */
    private static void prim(int[][] weight, char[] chars, int start) {
        //记录访问过的顶点
        int[] visited = new int[chars.length];
        //把当前节点记录为访问过
        visited[start] = 1;//1为访问过，0为未访问过
        int minweight = Integer.MAX_VALUE;
        int h1 = 0;
        int h2 = 0;
        //边数为顶点数-1
        for (int i = 0; i < chars.length - 1; i++) {
            //这个是确定每一次生成的子图 ，和哪个结点的距离最近
            for (int j = 0; j < weight.length; j++) {
                for (int k = 0; k < weight[j].length; k++) {
                    //寻找已经访问过的结点和未访问过的结点间的权值最小的边
                    if (visited[j] == 1 && visited[k] == 0 && minweight > weight[j][k]) {
                        minweight = weight[j][k];
                        h1 = j;
                        h2 = k;
                    }
                }
            }
            System.out.println("边<"+chars[h1]+","+chars[h2]+"> 权值"+minweight);
            characters.add(chars[h1]);
            //开始标记记录的minweight的坐标
            visited[h2] = 1;
            minweight = Integer.MAX_VALUE;
        }
    }
}

数组说明:因为每次迭代都是寻找已经访问过的结点和未访问过的结点间的权值最小的边。

如图: