Coursera 机器学习笔记（七）

主要为第九周内容：异常检测、推荐系统

（一）异常检测(DENSITY ESTIMATION)

核密度估计（kernel density estimation）是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。密度估计是指给定数据集 x(1),x(2),..,x(m)，我们假使数据集是正常的，我们希望知道新的数据 x(test)是不是异常的，即这个测试数据不属于该组数据的几率如何。我们所构建的模型应该能根据该测试数据的位置告诉我们其属于一组数据的可能性 p(x)。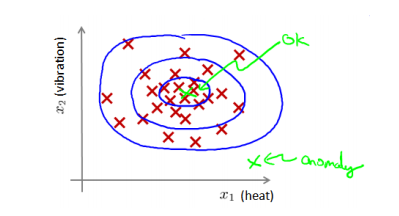

通过密度估计之后，选择一个概率阈值进行判断是否是异常，这也是异常检测中常用的方法。如：

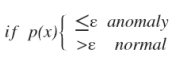
1. 高斯分布

   高斯核函数是核密度估计中常用的核函数。其中一元高斯概率密度函数为：

   

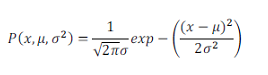
   可以利用已有的数据来预测总体中的μ和σ2的计算方法如下：

   

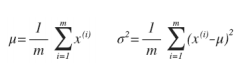
   多元高斯分布的概率密度函数为：

   

   

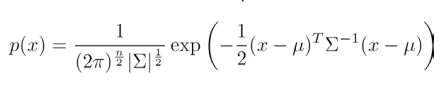
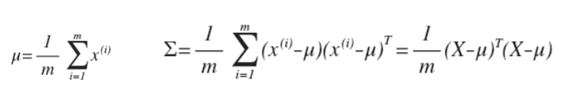
   如果训练集不是太大，并且没有太多的特征，我们可以使用多元高斯分布模型。

   注：机器学习中对于方差我们通常只除以 m 而非统计学中的（m-1）。

2. 异常检测

   首先，选择好训练的特征，对于异常检测算法，我们使用的特征是至关重要的，异常检测假设特征符合高斯分布，如果数据的分布不是高斯分布，异常检测算法也能够工作，但是最好还是将数据转换成高斯分布。，例如使用对数函数x = log(x+c)或者指数函数x=x^c。

   

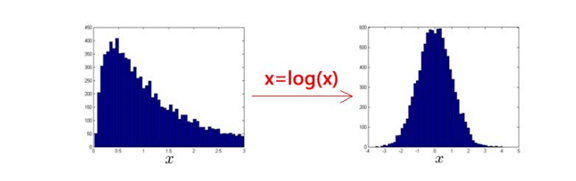
   选定好特征之后，一般的高斯分布模型中，对于给定的数据集 x(1),x(2),...,x(m) ，我们要针对每一个特征计算μ和σ2的估计值，根据模型计算 p(x)：

   

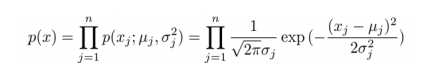
   如下图所示：

   

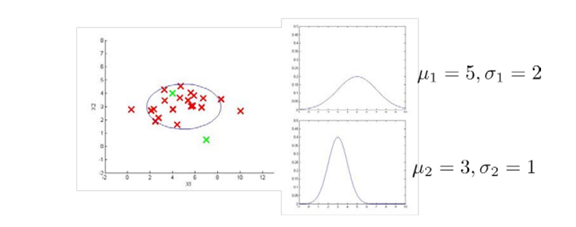
   对于多元高斯分布模型，首先计算所有特征的平均值，然后再计算协方差矩阵，最后我们计算多元高斯分布的 p(x)：

   

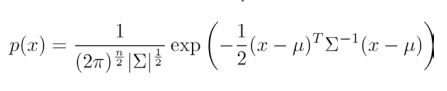
   选择一个ε，将 p(x)=ε作为我们的判定边界，当 p(x)>ε时预测数据为正常数据，否则为异常。

3. 构建系统

   1.获得大量标记的数据（异常或正常），然后选择其中一部分正常数据用于构建训练集，用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试集。

   2.根据训练集数据，我们估计特征的平均值和方差并构建 p(x)函数
   3.对交叉检验集，我们尝试使用不同的ε值作为阀值，并预测数据是否异常，根据 F1 值或者查准率与查全率的比例来选择ε
   4.选出ε后，针对测试集进行预测，计算异常检验系统的 F1 值或者查准率与查全率之比

4.对比

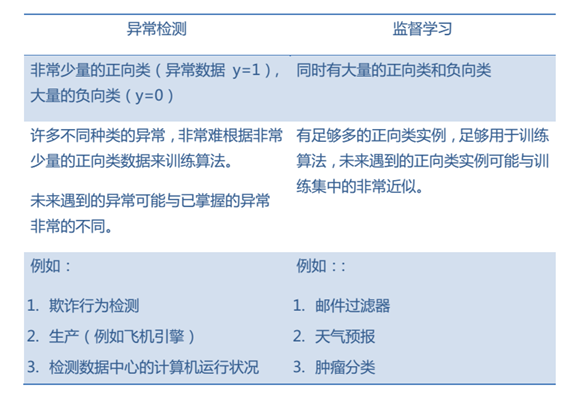
（二）推荐系统

推荐系统在生活中，无处不在。如电影有豆瓣电影、NetFilx，音乐平台网易云音乐、豆瓣FM、虾米等，网购淘宝、京东等等。

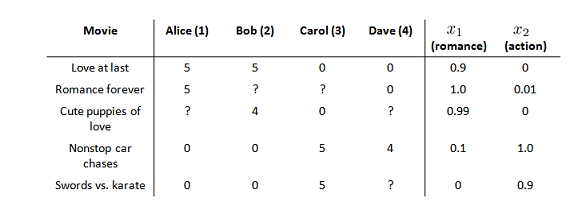
有 5 部电影和 4 个用户，我们要求用户为电影打分。前三部电影是爱情片，后两部则是动作片，我们可以看出 Alice 和 Bob 似乎更倾向与爱情片，而 Carol 和 Dave 似乎更倾向与动作片。并且没有一个用户给所有的电影都打过分。我们希望构建一个算法来预测他们每个人可能会给他们没看过的电影打多少分，并以此作为推荐的依据。

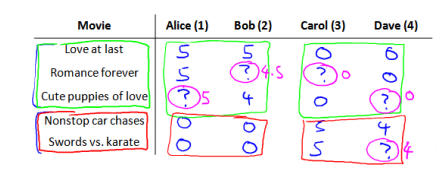
标记：nu代表用户的数量nm 代表电影的数量； r(i,j)如果用户 i 给电影 j 评过分则 r(i,j)=1；y(i,j)代表用户 i 给电影 j 的评分；mj 代表用户； j 评过分的电影的总数。

1. 基于内容

   基于内容的推荐(content-based recommendation)是指根据用户选择的对象,推荐其他类似属性的对象作为推荐，不需要依据其他用户对对象的评价意见。

   对象内容特征(Content(s))的选取也是重要研究。在之前，例子中，我们选取电影的两个特征： x1代表电影的浪漫程度，x2代表电影的动作程度。

   

   基于这些特征来构建一个推荐系统算法，采用线性回归模型，我们可以针对每一个用户都训练一个线性回归模型。对于用户 j 和电影 i，我们预测评分为：(θ(j))T(x(i))，其中θ(j)用户 j 的参数向量，x(i)电影 i 的特征向量。相应的j用户的模型的代价函数是：

   

   对于所有用户的代价函数为：

   

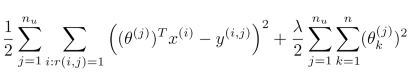
   可以通过梯度下降法来求解最优解。

   

   当然可以定义其他的参数模型，运用其他的机器学习方法。

2. 基于协同过滤

   在日常生活中，我们往往会利用好朋友的推荐来进行一些选择。协同过滤正是把这一思想运用到推荐系统中来，即基于其他用户对某一内容的评价向目标用户进行推荐。

   协同过滤算法可以同时学习用户的参数和电影的特征，对应的代价函数即优化目标为：

   

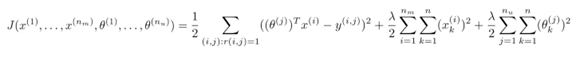
   利用梯度下降法最小化代价函数

   

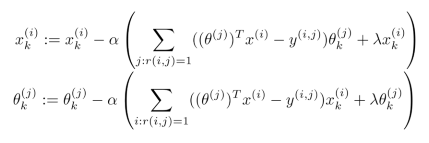
   在进行训练算法前，需要对结果Y矩阵进行均值归一化，如下图：

   

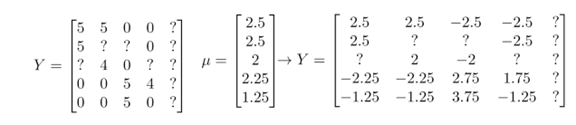
   然后利用这个新的Y矩阵来训练算法。最后预测值为预测(θ(j))T(x(i))+μi 。对于归一化的新模型，认为新用户对电影的评分都是电影的平均分。

    

参考：

[1].许海玲, 吴潇, 李晓东, 等. 互联网推荐系统比较研究[J]. 软件学报, 2009, 20(2): 350-362.

[2]. 李存华, 孙志挥, 陈耿, 等. 核密度估计及其在聚类算法构造中的应用[J]. 计算机研究与发展, 2004, 41(10): 1712-1719.

[3].博客：一维数据可视化：核密度估计http://www.lifelaf.com/blog/?p=723