Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
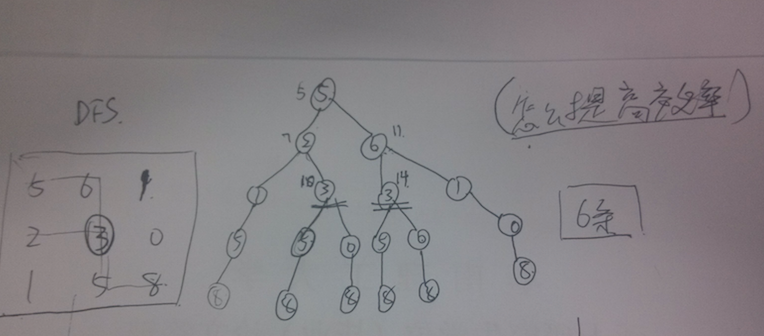
解法1:DFS,超时。
思路:其实类似对二叉树的DFS,只是终止条件不同,递归的终止条件就是到达最后一列,或者到达最后一行,因为最后一列的数字只有一个选择就是往下走,最后一行类似只有往右走。
当走到grid[rowMax-1][colMax-1],也就是一次路径完成,并和minSum做较,取较小的。
超时输入:
int my_grid[rowMax][colMax]={
{7,1,3,5,8,9,9,2,1,9,0,8,3,1,6,6,9,5},
{9,5,9,4,0,4,8,8,9,5,7,3,6,6,6,9,1,6},
{8,2,9,1,3,1,9,7,2,5,3,1,2,4,8,2,8,8},
{6,7,9,8,4,8,3,0,4,0,9,6,6,0,0,5,1,4},
{7,1,3,1,8,8,3,1,2,1,5,0,2,1,9,1,1,4},
{9,5,4,3,5,6,1,3,6,4,9,7,0,8,0,3,9,9},
{1,4,2,5,8,7,7,0,0,7,1,2,1,2,7,7,7,4},
{3,9,7,9,5,8,9,5,6,9,8,8,0,1,4,2,8,2},
{1,5,2,2,2,5,6,3,9,3,1,7,9,6,8,6,8,3},
{5,7,8,3,8,8,3,9,9,8,1,9,2,5,4,7,7,7},
{2,3,2,4,8,5,1,7,2,9,5,2,4,2,9,2,8,7},
{0,1,6,1,1,0,0,6,5,4,3,4,3,7,9,6,1,9}};
代码:
class Solution { private: int minSum; vector<vector<int>> my_grid; int rowMax; int colMax; public: void tra(int i,int j,int sum){ sum+=my_grid[i][j]; if(j==colMax-1&&i<rowMax) { ++i; for (i;i<rowMax;++i) { sum+=my_grid[i][j]; } if(i==rowMax&&sum<minSum){ minSum=sum; } return; } if(i==rowMax-1&&j<colMax) { ++j; for (j;j<colMax;++j) { sum+=my_grid[i][j]; } if(j==colMax&&sum<minSum){ minSum=sum; } return; } tra(i,j+1,sum); tra(i+1,j,sum); } int minPathSum(vector<vector<int>>& grid) { minSum=(~(unsigned int)0)>>1; my_grid=grid; rowMax=grid.size(); colMax=grid[0].size(); tra(0,0,0); return minSum; } };
解法2:DP(还是不熟练,不太熟练递推dp和递归dp的区别,参考文章)
dp[100][100];该dp数组记录的是每个位置上的最优解,即到达这一点的路径最小值。假设我们要求以grid[i][j]为末尾的最小路径值,我们只需要求出它头上一个格子,和左边格子为末尾的最小路径值之中的最小值,也即min{dp[i-1][j],dp[i][j-1]}.
所以综合下,动态转移方程就是dp[i][j]=min{dp[i-1][j],dp[i][j-1]}+grid[i][j];

代码:
class Solution { public: int minPathSum(vector<vector<int> > &grid) { if(grid.size()==0) return 0; vector<vector<int>> res(grid); int i, j; for(int j=1; j<res[0].size(); ++j){ res[0][j] += res[0][j-1]; } for(int j=1; j<res.size(); ++j){ res[j][0] += res[j-1][0]; } for(i=1; i<res.size(); ++i){ for(int j=1; j<res[i].size(); ++j){ res[i][j] = min(res[i-1][j], res[i][j-1])+grid[i][j]; } } return res[grid.size()-1][grid[0].size()-1]; //注意行列的size不一定一样 } };