Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.
For example, given the following matrix:
1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0
Return 4.
思路:DP。
我们维护一个二维数组dp[i][j],它所维护的内容是以点(i, j)为右下角顶点的最大正方形的边长。
先考虑初始情况,对于矩阵最上面一行(即i = 0时), dp[i][j] = matrix[i][j]。对于矩阵最左侧那一列(即j = 0时),dp[i][j] = matrix[i][j]。原因很简单,对于矩阵最上面一行和最左侧一列,当点为0时,不存在包含该点的正方形,因为dp数组的值也为0;当点为1时,则包含该点的正方形边长最大即为1,因为点在矩阵边界,无法再继续扩大正方形的大小了。
现在考虑普遍情况,即i > 0, j > 0时。此时,若matrix[i][j] = 0, 则dp[i][j] = 0。因为没有正方形包含这点。
若matrix[i][j] = 1时,递推公式如下:
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1.
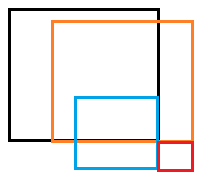
图中红色正方形为现在的位置(i, j),已知其为1。则其所能构成的正方形大小由左侧,上侧,左上侧三个正方形的最小边长所决定。这也就是递推公式的含义。
在实现过程中,dp数组我用滚动数组实现。
1 class Solution { 2 public: 3 int maximalSquare(vector<vector<char>>& matrix) { 4 int n = matrix.size(); 5 if (n == 0) return 0; 6 int m = matrix[0].size(); 7 vector<int> tem(m, 0); 8 vector<vector<int> > dp(2, tem); 9 int res = 0; 10 for (int i = 0; i < m; i++) 11 { 12 dp[0][i] = (int)(matrix[0][i] - '0'); 13 res = max(res, dp[0][i]); 14 } 15 for (int i = 1; i < n; i++) 16 for (int j = 0; j < m; j++) 17 { 18 if (matrix[i][j] == '0') 19 dp[i % 2][j] = 0; 20 else if (j == 0) 21 { 22 dp[i % 2][j] = 1; 23 res = max(dp[i % 2][j], res); 24 } 25 else 26 { 27 dp[i % 2][j] = imin(dp[(i - 1) % 2][j], dp[i % 2][j - 1], dp[(i - 1) % 2][j - 1]) + 1; 28 res = max(dp[i % 2][j], res); 29 } 30 } 31 return res * res; 32 } 33 int imin(int a, int b, int c) 34 { 35 int res = a < b ? a : b; 36 return res < c ? res : c; 37 } 38 };