[Hnoi2014]世界树
Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 1921 Solved: 1019
[Submit][Status][Discuss]
Description
世界树是一棵无比巨大的树,它伸出的枝干构成了整个世界。在这里,生存着各种各样的种族和生灵,他们共同信奉着绝对公正公平的女神艾莉森,在他们的信条里,公平是使世界树能够生生不息、持续运转的根本基石。
世界树的形态可以用一个数学模型来描述:世界树中有n个种族,种族的编号分别从1到n,分别生活在编号为1到n的聚居地上,种族的编号与其聚居地的编号相同。有的聚居地之间有双向的道路相连,道路的长度为1。保证连接的方式会形成一棵树结构,即所有的聚居地之间可以互相到达,并且不会出现环。定义两个聚居地之间的距离为连接他们的道路的长度;例如,若聚居地a和b之间有道路,b和c之间有道路,因为每条道路长度为1而且又不可能出现环,所卧a与c之间的距离为2。
出于对公平的考虑,第i年,世界树的国王需要授权m[i]个种族的聚居地为临时议事处。对于某个种族x(x为种族的编号),如果距离该种族最近的临时议事处为y(y为议事处所在聚居地的编号),则种族x将接受y议事处的管辖(如果有多个临时议事处到该聚居地的距离一样,则y为其中编号最小的临时议事处)。
现在国王想知道,在q年的时间里,每一年完成授权后,当年每个临时议事处将会管理多少个种族(议事处所在的聚居地也将接受该议事处管理)。 现在这个任务交给了以智慧著称的灵长类的你:程序猿。请帮国王完成这个任务吧。
Input
第一行为一个正整数n,表示世界树中种族的个数。
接下来n-l行,每行两个正整数x,y,表示x聚居地与y聚居地之间有一条长度为1的双
向道路。接下来一行为一个正整数q,表示国王询问的年数。
接下来q块,每块两行:
第i块的第一行为1个正整数m[i],表示第i年授权的临时议事处的个数。
第i块的第二行为m[i]个正整数h[l]、h[2]、…、h[m[i]],表示被授权为临时议事处的聚居地编号(保证互不相同)。
Output
输出包含q行,第i行为m[i]个整数,该行的第j(j=1,2…,,m[i])个数表示第i年被授权的聚居地h[j]的临时议事处管理的种族个数。
Sample Input
2 1
3 2
4 3
5 4
6 1
7 3
8 3
9 4
10 1
5
2
6 1
5
2 7 3 6 9
1
8
4
8 7 10 3
5
2 9 3 5 8
Sample Output
3 1 4 1 1
10
1 1 3 5
4 1 3 1 1
HINT
N<=300000, q<=300000,m[1]+m[2]+…+m[q]<=300000
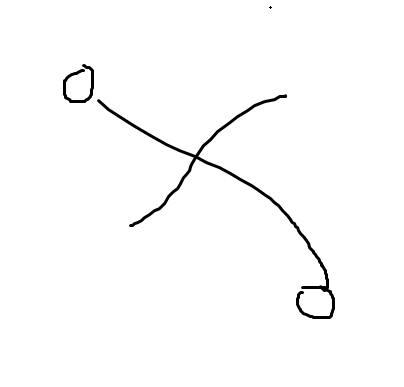
是有一条分界线的,这个很好想的,
然后就是去寻找这个分界线在哪里。
不能直接去寻找,会出现极端情况,
需要倍增去寻找。
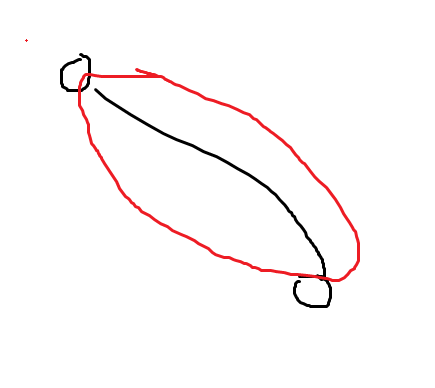
处理完红色部分,最后处理两个点中的。
根据sz来减,应该很好想的,代码注释了不少。
1 #include<cstring> 2 #include<cmath> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstdio> 6 7 #define N 300007 8 using namespace std; 9 inline int read() 10 { 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 13 while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 17 int n,q,m,tot,tim,tim1; 18 int cnt,hed[N],nxt[N*2],rea[N*2];//原来的边表 19 int cnt1,hed1[N],nxt1[N*2],rea1[N*2];//另外一个边表 20 int id[N],sz[N],fa[N][20],deep[N];//dfs序,大小,父亲,深度 21 int a[N],out[N],bel[N],virt[N],num[N],sta[N],dis[N],ans[N];//输入的,输出的。属于哪个关键点 22 //虚树的顺序。自己的个数。建虚树的栈,记录和关键点距离,答案。 23 24 void add(int u,int v) 25 { 26 nxt[++cnt]=hed[u]; 27 hed[u]=cnt; 28 rea[cnt]=v; 29 } 30 void add1(int u,int v) 31 { 32 nxt1[++cnt1]=hed1[u]; 33 hed1[u]=cnt1; 34 rea1[cnt1]=v; 35 } 36 void dfs(int u) 37 { 38 id[u]=++tim,sz[u]=1; 39 for (int i=1;i<=19;i++)fa[u][i]=fa[fa[u][i-1]][i-1]; 40 for (int i=hed[u];i!=-1;i=nxt[i]) 41 { 42 int v=rea[i]; 43 if (v==fa[u][0])continue; 44 fa[v][0]=u,deep[v]=deep[u]+1,dfs(v); 45 sz[u]+=sz[v]; 46 } 47 } 48 int lca(int a,int b) 49 { 50 if (deep[a]<deep[b])swap(a,b); 51 int i; 52 for (i=0;(1<<i)<=deep[a];i++);i--; 53 for (int j=19;j>=0;j--) 54 if (deep[a]-(1<<j)>=deep[b])a=fa[a][j]; 55 if (a==b) return a; 56 for (int j=19;j>=0;j--) 57 if (fa[a][j]!=fa[b][j]) a=fa[a][j],b=fa[b][j]; 58 return fa[a][0]; 59 } 60 bool cmp(int x,int y)//按照dfs序大小 61 { 62 return id[x]<id[y]; 63 } 64 int sue_dis(int a,int b)//得到距离 65 { 66 return deep[a]+deep[b]-2*deep[lca(a,b)]; 67 } 68 //dfs1+dfs2是处理虚树上所以点被哪个关键点所包含。 69 void dfs1(int u)//处理儿子对于父亲的 70 { 71 virt[++tim1]=u,num[u]=sz[u]; 72 for (int i=hed1[u];i!=-1;i=nxt1[i]) 73 { 74 int v=rea1[i]; 75 dfs1(v); 76 int t1=dis[u],t2=sue_dis(u,bel[v]); 77 if (t1>t2||(t1==t2&&bel[u]>bel[v])||!bel[u]) 78 { 79 dis[u]=t2; 80 bel[u]=bel[v]; 81 } 82 } 83 } 84 void dfs2(int u)//处理父亲对于儿子的 85 { 86 for (int i=hed1[u];i!=-1;i=nxt1[i]) 87 { 88 int v=rea1[i]; 89 int t1=sue_dis(bel[u],v),t2=dis[v]; 90 if (t2>t1||(t2==t1&&bel[u]<bel[v])) 91 { 92 dis[v]=t1; 93 bel[v]=bel[u]; 94 } 95 dfs2(v); 96 } 97 } 98 void solve(int a,int b)//处理相邻点对 99 { 100 int x=b,mid=b; 101 for (int i=19;i>=0;i--) 102 if (deep[fa[x][i]]>deep[a]) x=fa[x][i]; 103 num[a]-=sz[x]; 104 if (bel[a]==bel[b]) 105 { 106 ans[bel[a]]+=sz[x]-sz[b]; 107 return; 108 } 109 for (int i=19;i>=0;i--) 110 { 111 int wei=fa[mid][i]; 112 if (deep[wei]<deep[a]) continue; 113 int t1=sue_dis(bel[a],wei),t2=sue_dis(bel[b],wei); 114 if (t1>t2||(t1==t2&&bel[b]<bel[a])) mid=wei; 115 } 116 ans[bel[a]]+=sz[x]-sz[mid]; 117 ans[bel[b]]+=sz[mid]-sz[b]; 118 } 119 void build_and_solve() 120 { 121 m=read(); 122 for (int i=1;i<=m;i++) 123 out[i]=a[i]=read(),bel[a[i]]=a[i]; 124 sort(a+1,a+m+1,cmp); 125 tot=0; 126 if (a[1]!=1) sta[++tot]=1; 127 for (int i=1;i<=m;i++) 128 { 129 int t=a[i],f=0,flag=0; 130 while(tot>0) 131 { 132 flag=1; 133 f=lca(t,sta[tot]); 134 // if (f==0) cout<<tot<<" "<<sta[tot]<<" "<<t<<endl; 135 if (tot>1&&deep[f]<deep[sta[tot-1]]) 136 { 137 add1(sta[tot-1],sta[tot]); 138 tot--; 139 } 140 else if (deep[f]<deep[sta[tot]]) 141 { 142 add1(f,sta[tot]); 143 tot--; 144 break; 145 } 146 else break; 147 } 148 if (sta[tot]!=f) sta[++tot]=f; 149 // if (flag&&sta[tot]==0) cout<<"gg"<<" "<<t<<" "<<sta[tot]<<" "<<tot<<endl; 150 sta[++tot]=t; 151 } 152 while(tot>1) 153 { 154 add1(sta[tot-1],sta[tot]); 155 tot--; 156 } 157 dfs1(1); 158 dfs2(1); 159 for (int i=1;i<=tim1;i++) 160 for (int j=hed1[virt[i]];j!=-1;j=nxt1[j]) 161 { 162 int v=rea1[j]; 163 solve(virt[i],v); 164 } 165 for (int i=1;i<=tim1;i++) 166 ans[bel[virt[i]]]+=num[virt[i]]; 167 for (int i=1;i<=m;i++) 168 { 169 printf("%d ",ans[out[i]]); 170 //if (i==m) printf(" "); 171 //else printf(" "); 172 } 173 cout<<endl; 174 cnt1=0; 175 for (int i=1;i<=tim1;i++) 176 hed1[virt[i]]=-1,num[virt[i]]=dis[virt[i]]=bel[virt[i]]=0,virt[i]=0; 177 tim1=0; 178 for (int i=1;i<=m;i++) 179 ans[a[i]]=0; 180 } 181 int main() 182 { 183 freopen("fzy.in","r",stdin); 184 freopen("fzy.out","w",stdout); 185 186 memset(hed,-1,sizeof(hed)); 187 memset(hed1,-1,sizeof(hed1)); 188 int n=read(); 189 for (int i=1;i<n;i++) 190 { 191 int u=read(),v=read(); 192 add(u,v),add(v,u); 193 } 194 deep[1]=1,dfs(1); 195 q=read(); 196 while(q--) 197 { 198 build_and_solve(); 199 } 200 }