切蛋糕（二分）（二维前缀和）

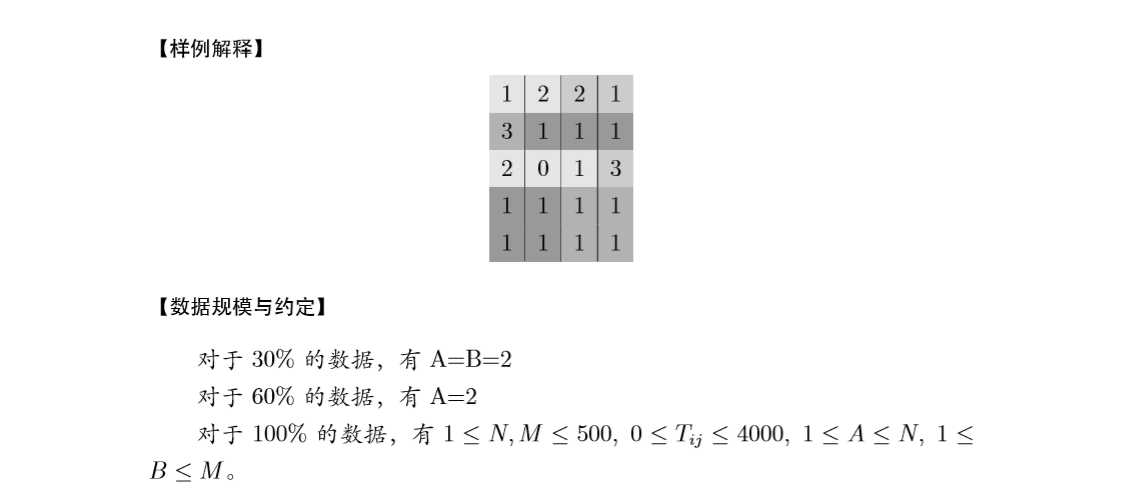
观察数据范围，n*m比较小，所以我们预先处理出前缀和。

然后我们可以考虑写一个函数来计算二维前缀和（二维前缀和大家都会的吧qwq，那我就不说了，就是要注意一下哪个是横轴哪个是纵轴）

之后就是二维上的二分位置，然后check看看符不符合二分出来的ans。

• 注：一半求最大化最小值和最小化最大值的问题，都可以往二分想。我们可以把最优化问题二分后来check转化为判定问题。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 550
using namespace std;
int n,m,lx,rx,ly,ry,aa,bb;
ll sum[maxn][maxn]; 

bool calc(int lx,int down,int rx,int up,int num)
	{return (sum[rx][up]-sum[rx][down-1]-sum[lx-1][up]+sum[lx-1][down-1])>=num;}
	
bool check2(int num){
    bool yes=1;ly=ry=1;
    for(int j=1;j<=bb;j++)
	{
        while(ry+1<=m&&!calc(lx,ly,rx,ry,num))
			ry++;
        if(!calc(lx,ly,rx,ry,num))
			{yes=0;break;}
        ly=++ry;
    }
    return yes;
}
bool check(int num){
    bool flag=1;
    lx=1,rx=1;
    for(int i=1;i<=aa;i++)
	{
        while(rx+1<=n&&!check2(num)) 
			rx++;
        if(!check2(num))
			{flag=0;break;}
        lx=++rx;
    }
    if(flag==1) return true;
    else return false;
}   
int main(){
    freopen("champion.in","r",stdin);
    freopen("champion.out","w",stdout);
	scanf("%d%d%d%d",&n,&m,&aa,&bb);
    for(int i=1;i<=n;i++)
	{
        for(int j=1;j<=m;j++)
		{
			int cur;
			scanf("%d",&cur);
			sum[i][j]=sum[i][j-1]+cur;
		}
        for(int j=1;j<=m;j++) sum[i][j]+=sum[i-1][j];
    }
    //前缀和 
    long long l=0,r=sum[n][m],mid;
    //二分可以取到的答案qwq 
    while(l<r)
	{
        mid=(l+r)>>1;
        if(check(mid))
			l=mid+1;
		else r=mid;
    }
    printf("%lld
",l-1);
    return 0;
}