https://www.cnblogs.com/xiohao/p/9054355.html
一,对称加密
所谓对称加密,就是它们在编码时使用的密钥e和解码时一样d(e=d),我们就将其统称为密钥k。
对称加解密的过程如下:
发送端和接收端首先要共享相同的密钥k(即通信前双方都需要知道对应的密钥)才能进行通信。发送端用共享密钥k对明文p进行加密,得到密文c,并将得到的密文发送给接收端,接收端收到密文后,并用其相同的共享密钥k对密文进行解密,得出明文p。
一般加密和解密的算法是公开的,需要保持隐秘的是密钥k,流行的对称加密算法有:DES,Triple-DES,RC2和RC4
对称加密的不足主要有两点:
1,发送方和接收方首先需要共享相同的密钥,即存在密钥k的分发问题,如何安全的把共享密钥在双方进行分享,这本身也是一个如何安全通信的问题,一种方法是提前双方约定好,不通过具体的通信进行协商,避免被监听和截获。另外一种方式,将是下面我们介绍的通过非对称加密信道进行对称密码的分发和共享,即混合加密系统。
2,密钥管理的复杂度问题。由于对称加密的密钥是一对一的使用方式,若一方要跟n方通信,则需要维护n对密钥。
对称加密的好处是:
加密和解密的速度要比非对称加密快很多,因此常用非对称加密建立的安全信道进行共享密钥的分享,完成后,具体的加解密则使用对称加密。即混合加密系统。
另外一个点需要重点说明的是,密钥k的长度对解密破解的难度有很重大的影响,k的长度越长,对应的密码空间就越大,遭到暴力破解或者词典破解的难度就更大,就更加安全。
二,非对称加密
所谓非对称加密技术是指加密的密钥e和解密的密钥d是不同的(e!=d),并且加密的密钥e是公开的,叫做公钥,而解密的密钥d是保密的,叫私钥。
非对称加解密的过程如下:
加密一方找到接收方的公钥e(如何找到呢?大部分的公钥查找工作实际上都是通过数字证书来实现的),然后用公钥e对明文p进行加密后得到密文c,并将得到的密文发送给接收方,接收方收到密文后,用自己保留的私钥d进行解密,得到明文p,需要注意的是:用公钥加密的密文,只有拥有私钥的一方才能解密,这样就可以解决加密的各方可以统一使用一个公钥即可。
常用的非对称加密算法有:RSA
非对称加密的优点是:
1,不存在密钥分发的问题,解码方可以自己生成密钥对,一个做私钥存起来,另外一个作为公钥进行发布。
2,解决了密钥管理的复杂度问题,多个加密方都可以使用一个已知的公钥进行加密,但只有拥有私钥的一方才能解密。
非对称加密不足的地方是加解密的速度没有对称加密快。
综上,分析了对称加密和非对称加密各自的优缺点后,有没有一种办法是可以利用两者的优点但避开对应的缺点呢?答应是有的,实际上用得最多的是混合加密系统,比如在两个节点间通过便捷的公开密码加密技术建立起安全通信,然后再用安全的通信产生并发送临时的随机对称密钥,通过更快的对称加密技术对剩余的数据进行加密。
SSL协议通信过程
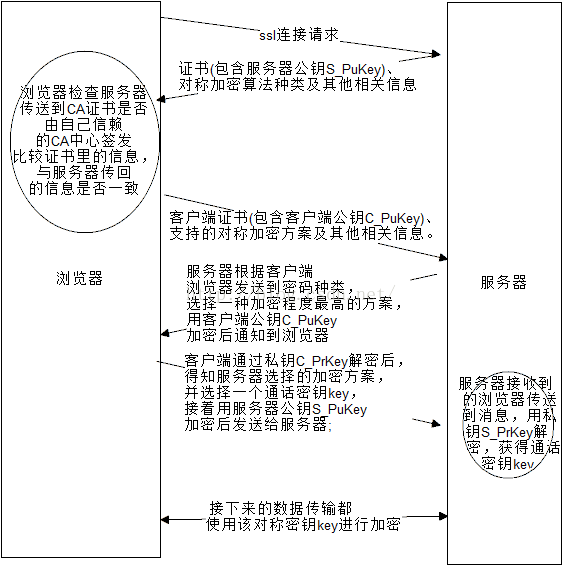
(1) 浏览器发送一个连接请求给服务器;服务器将自己的证书(包含服务器公钥S_PuKey)、对称加密算法种类及其他相关信息返回客户端;
(2) 客户端浏览器检查服务器传送到CA证书是否由自己信赖的CA中心签发。若是,执行4步;否则,给客户一个警告信息:询问是否继续访问。
(3) 客户端浏览器比较证书里的信息,如证书有效期、服务器域名和公钥S_PK,与服务器传回的信息是否一致,如果一致,则浏览器完成对服务器的身份认证。
(4) 服务器要求客户端发送客户端证书(包含客户端公钥C_PuKey)、支持的对称加密方案及其他相关信息。收到后,服务器进行相同的身份认证,若没有通过验证,则拒绝连接;
(5) 服务器根据客户端浏览器发送到密码种类,选择一种加密程度最高的方案,用客户端公钥C_PuKey加密后通知到浏览器;
(6) 客户端通过私钥C_PrKey解密后,得知服务器选择的加密方案,并选择一个通话密钥key,接着用服务器公钥S_PuKey加密后发送给服务器;
(7) 服务器接收到的浏览器传送到消息,用私钥S_PrKey解密,获得通话密钥key。
(8) 接下来的数据传输都使用该对称密钥key进行加密。
上面所述的是双向认证 SSL 协议的具体通讯过程,服务器和用户双方必须都有证书。由此可见,SSL协议是通过非对称密钥机制保证双方身份认证,并完成建立连接,在实际数据通信时通过对称密钥机制保障数据安全性