1. 前言
Java Stream Api 提供了很多有用的 Api 让我们很方便将集合或者多个同类型的元素转换为流进行操作。今天我们来看看如何合并 Stream 流。
2. Stream 流的合并
Stream 流合并的前提是元素的类型能够一致。
2.1 concat
最简单合并流的方法是通过 Stream.concat() 静态方法:
Stream<Integer> stream = Stream.of(1, 2, 3);
Stream<Integer> another = Stream.of(4, 5, 6);
Stream<Integer> concat = Stream.concat(stream, another);
List<Integer> collect = concat.collect(Collectors.toList());
List<Integer> expected = Lists.list(1, 2, 3, 4, 5, 6);
Assertions.assertIterableEquals(expected, collect);
这种合并是将两个流一前一后进行拼接:
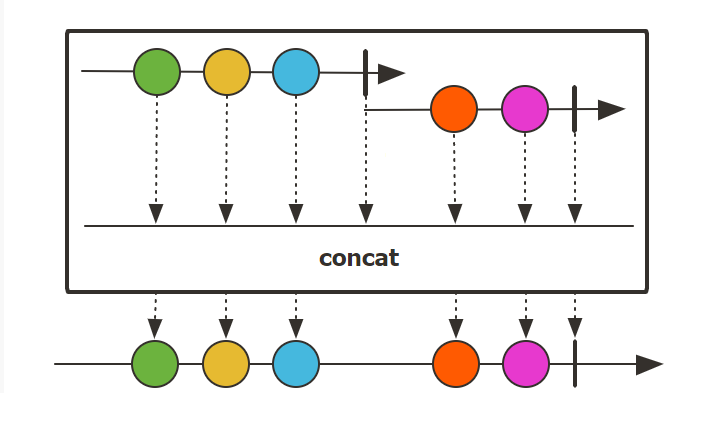
2.2 多个流的合并
多个流的合并我们也可以使用上面的方式进行“套娃操作”:
Stream.concat(Stream.concat(stream, another), more);
你可以一层一层继续套下去,如果需要合并的流多了,看上去不是很清晰。
我之前介绍过一个Stream 的 flatmap 操作 ,它的大致流程可以参考里面的这一张图:

因此我们可以通过 flatmap 进行实现合并多个流:
Stream<Integer> stream = Stream.of(1, 2, 3);
Stream<Integer> another = Stream.of(4, 5, 6);
Stream<Integer> third = Stream.of(7, 8, 9);
Stream<Integer> more = Stream.of(0);
Stream<Integer> concat = Stream.of(stream,another,third,more).
flatMap(integerStream -> integerStream);
List<Integer> collect = concat.collect(Collectors.toList());
List<Integer> expected = Lists.list(1, 2, 3, 4, 5, 6, 7, 8, 9, 0);
Assertions.assertIterableEquals(expected, collect);
这种方式是先将多个流作为元素生成一个类型为 Stream<Stream<T>> 的流,然后进行 flatmap 平铺操作合并。
2.3 第三方库
有很多第三方的强化库 StreamEx 、Jooλ 都可以进行合并操作。另外反应式编程库 Reactor 3 也可以将 Stream 流合并为反应流,在某些场景下可能会有用。这里演示一下:
List<Integer> block = Flux.fromStream(stream)
.mergeWith(Flux.fromStream(another))
.collectList()
.block();
3. 总结
如果你经常使用 Java Stream Api ,合并 Stream 流是经常遇到的操作。今天简单介绍了合并 Stream 流的方式,希望对你有用。我是 码农小胖哥 ,多多关注!更多干货奉上。
关注公众号:Felordcn 获取更多资讯