首先是几个名词:
时域:时域是描述数学函数或物理信号对时间的关系,我们在实际中对信号物理量的描述都是以时间为基准的,沿着时间增加的方向我们才有了波形周期、波形的概念,从以时间为角度称为时域。
频域:频域分析是把信号变为以频率轴为坐标表示出来。也即从频率的角度去描述波形。
时域分析与频域分析是对模拟信号的两个观察面,根据傅立叶分析,所有的波形都可以分解为正弦波,可以由不同频率的正弦波叠加而成,一种频率的正弦波在频域上对应一个点,就行时域上的时间点一样。例如下图波形,从时域上看是类似方波,二如果从频域上看就是一个个线段。

傅立叶变换:将时域上的波形分解成正弦波的过程就是傅立叶变换,傅立叶正变换可以将波形分解,投影到频域上,傅立叶逆变换可以将频域上波形叠加,映射到时域上。变换过程如下图所示:
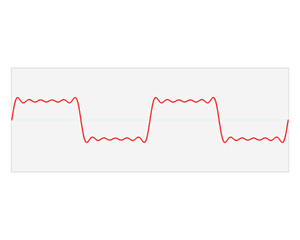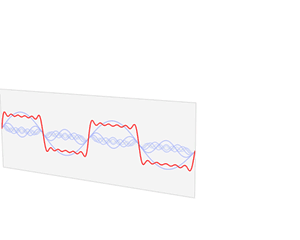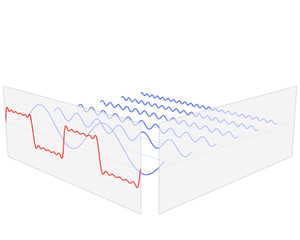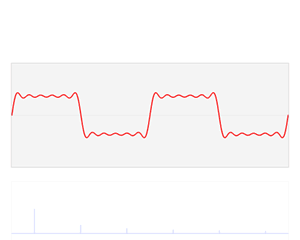
为何要进行傅立叶变换?
很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。离散傅里叶变换(DFT)是傅里叶变换在离散系统中的表示形式。但是DFT的计算量非常大, FFT就是DFT的一种快速算法。
matlab实现:
我们对函数x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)进行FFT变换,并绘制出变换之前和之后的图像。

fs=100;N=1024;n=0:N-1;t=n/fs; x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号函数 subplot(2,1,1),plot(t,x); %绘出信号曲线 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求取Fourier变换的振幅 f=n*fs/N; %求频率 subplot(2,1,2),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on;
结果如下,我们可以看出上方是时域波形,下方是频域波形:
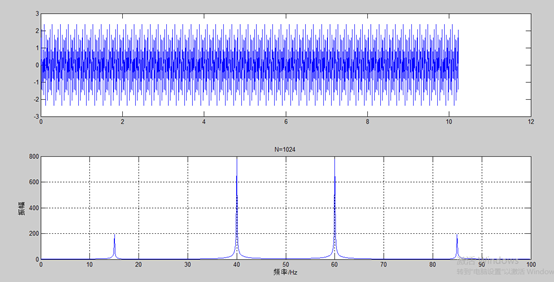
傅立叶变换的缺点:
基于傅里叶(Fourier)变换的信号频域表示,揭示了时间函数和频谱函数之间的内在联系,但是基于傅里叶变换的信号频域表示,揭示了时间函数和频谱函数之间的内在联系。傅里叶变换可以完成从时域到频域的转换(正变换),也可以完成从频域到时域的转换(逆变换),但不能同时具有时域和频域信息,而且傅立叶变换还有一个很大的缺点就是不能很好的处理突变。
为何同时需要时域和频域信息?
现实中大部分波形都是非稳态波形,频域信息只提供了波形的成分,并没有提供成分出现的先后,因此单纯的傅立叶分析对频率随时间变化的非平稳信号分辨率差。如下图所示:
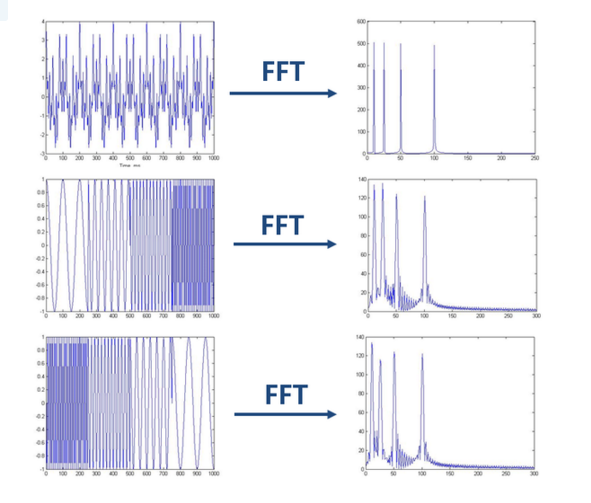
做FFT后,我们发现这三个时域上有巨大差异的信号,频谱(幅值谱)却非常一致。尤其是下边两个非平稳信号,我们从频谱上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同。

傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度就对应于频率(反比),平移量τ就对应于时间,小波分析的过程就是用单个小波不断伸缩平移,叠加出时域上的完整波形。
傅立叶变换与小波分析的区别:
傅立叶变换适合周期性的数据,分析不随时间变化的信号,小波不但适用此类信号,更能很好的处理突变信号以及非稳态信号。
小波:均值为0的一类波形,如图

小波分析:将原来的信号分解为基于小波波形经过平移和比例变化之后的一系列波形。小波变换分成两个大类:离散小波变换(DWT) 和连续小波变换(CWT)。两者的主要区别在于,连续变换在所有可能的缩放和平移上操作,而离散变换采用所有缩放和平移值的特定子集。一般来说,对于连续信号采用连续小波变换,对于离散信号采用离散小波变换。
母小波:母小波是一类具有快速衰减有限长的波函数
基小波(小波基):母函数伸缩、平移得到的一系列函数就是小波基函数,如下图就是小波基,常用的小波基有:Haar小波基、db系列小波基、Biorthogonal(biorNr.Nd)小波系、Coiflet(coifN)小波系、SymletsA(symN)小波系、Molet(morl)小波、Mexican Hat (mexh)小波、Meyer小波等。
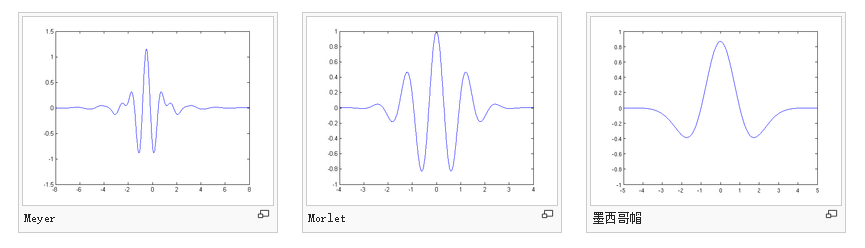
Matlab代实现:
名词:
离散小波变换、二进制小波与连续小波变换(DWT和CWT):三者的主要区别不是信号的离散,因为输入计算机的必然是离散信号,连续与离散是指尺度和平移量的取值是否离散。连续小波是尺度可连续取值的小波,里面的a一般取整数,而不像二进小波a取2的整数幂。从连续小波到二进小波再到正交离散小波,其实就是a、b都连续,a不连续、b连续,a、b都不连续的过程。在MATLAB里,也就是CWT,SWT,DWT。
近似系数和细节系数:可以理解为信号分离之后的低频部分和高频部分。
主要常用的函数如下:
wavedemo ;小波工具箱函数demo
cwt ;一维连续小波变换
dwt 单尺度一维离散小波变换,对离散小波单层分解
分析之前的图形:
t=0:0.03:2*pi;
y=sin(t.^2);
plot(t,y);

分析之后的图形:
a=1:32;
z=cwt(y,a,'mexh',plot)

三维显示:
代码:
surf(t,a,z)
shading flat;
axis([0 2*pi,0,32,min(z(:)) max(z(:))])
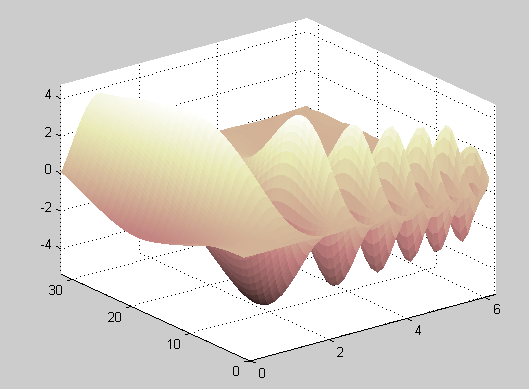
例子:离散小波,一般来说,离散小波分析用的较多,因为方便后续进行分析,离散小波采用dwt函数,调用形式为[cA,cD]=dwt(X,'wname'),使用wavemngr ;小波管理函数可列出所有可调用小波。
调用命令如下:
wavemngr('read',1)
结果:

小波模板数据采用wavefun函数绘制波形,此处不再绘制
我们一般采用Daubechies簇的小波,,db1也即haar小波,离散小波代码如下:

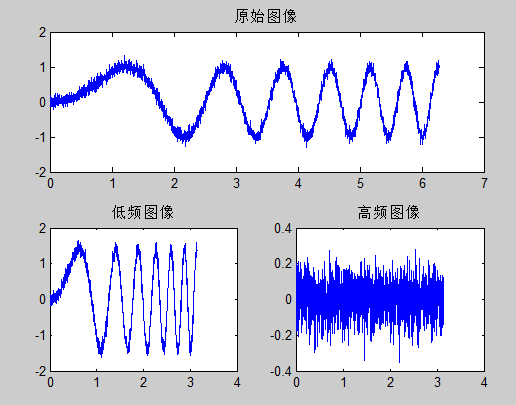
x=0:0.002:2*pi; y=sin(x.^2);%原始信号波形 r=0.1*randn(size(x)); y1=y+r; subplot(211); plot(x,y1); title('原始图像'); [cA,cD]=dwt(y1,'db4');%离散小波变换 subplot(223), plot(x(1:length(cA)),cA); title('低频图像'); subplot(224), plot(x(1:length(cD)),cD); title('高频图像'); %离散小波逆变换,并检验精度 y2=idwt(cA,cD,'db4'); ans=norm(y1-y2)
离散结果:
逆变误差:
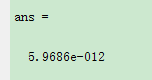
例子:一维小波信号的多层分解:
[C,L]=wavedec(x,n,fun),x为原始信号,n为分解步数,fun为所选用基小波的名称,C、L为分解后的两个向量,C、L两个向量的近似系数和细节系数的提取需要利用appcoef()和detcoef()完成。调用格式为:cA=appcoef(C,L,fun,n);以及cD=detcoef(C,L,i);提取第i段细节系数。重建函数采用wrcoef(),调用格式为:x=wrcoef(类型,C,L,fun,n);其中类型可选'a'或者'd',选择利用近似系数还是细节系数进行源信号构建,选择近似系数对去噪有很好的效果。
matlab代码如下:

%一维离散小波多层分解 clc;clear; x=0:0.002:2*pi; y=sin(x.^2);%原始信号波形 r=0.1*randn(size(x)); y1=y+r; subplot(411); plot(x,y1); title('原始图像'); %信号重构 [C,L]=wavedec(y1,3,'db6'); y2 = waverec(C,L,'db6') subplot(412); plot(x,y2); title('重构图像'); %高低频信号重建 y3=wrcoef('a',C,L,'db6',3) subplot(413); plot(x,y3); title('低频重建图像'); y4=wrcoef('a',C,L,'db6',3) subplot(414); plot(x,y4); title('高频重建图像'); figure(2); %下面为各层系数 cA1=appcoef(C,L,'db6',1); subplot(611); plot(cA1) title('一层分解低频图像'); cD1=detcoef(C,L,1); subplot(612); plot(cD1) title('一层分解高频图像'); cA2=appcoef(C,L,'db6',2); subplot(613); plot(cA2) title('二层分解低频图像'); cD2=detcoef(C,L,2); subplot(614); plot(cD2) title('二层分解高频图像'); cA3=appcoef(C,L,'db6',3); subplot(615); plot(cA3) title('三层分解低频图像'); cD3=detcoef(C,L,3); subplot(616); plot(cD3) title('三层分解高频图像');
运行结果:
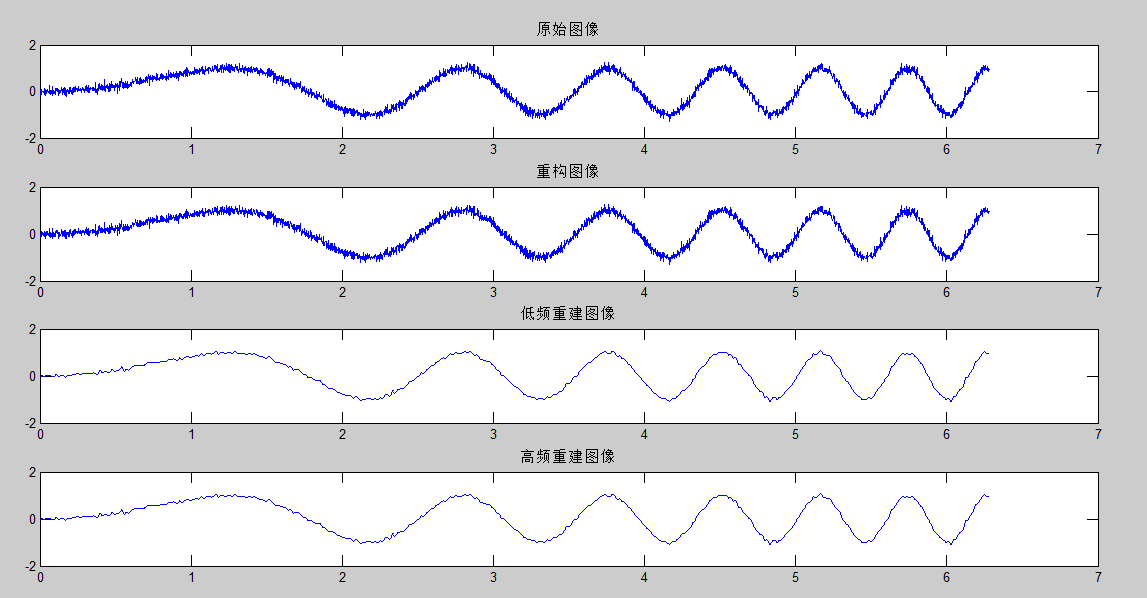

此外还可以使用wavemenu小波工具箱命令,通过界面的方式进行分析。
还需研究的问题:
1.基小波的选择,什么情况下选什么基小波,目前看来差别是不大的,选择常用就好
2.多层分解步数的确定是如何确定的
