（数据科学学习手札16）K-modes聚类法的简介&Python与R的实现

我们之前经常提起的K-means算法虽然比较经典，但其有不少的局限，为了改变K-means对异常值的敏感情况，我们介绍了K-medoids算法，而为了解决K-means只能处理数值型数据的情况，本篇便对K-means的变种算法——K-modes进行简介及Python、R的实现：

K-modes是数据挖掘中针对分类属性型数据进行聚类采用的方法，其算法思想比较简单，时间复杂度也比K-means、K-medoids低，大致思想如下：

假设有N个样本，共有M个属性，均为离散的，对于聚类数目标K：

step1：随机确定k个聚类中心C1,C2...Ck，Ci是长度为M的向量，Ci=[C1i,C2i,...,CMi]

step2：对于样本xj(j=1,2,...,N)，分别比较其与k个中心之间的距离（这里的距离为不同属性值的个数，假如x1=[1,2,1,3],C1=[1,2,3,4]x1=[1,2,1,3],C1=[1,2,3,4]，那么x1与C1之间的距离为2）

step3：将xj划分到距离最小的簇，在全部的样本都被划分完毕之后，重新确定簇中心，向量Ci中的每一个分量都更新为簇i中的众数

step4：重复步骤二和三，直到总距离（各个簇中样本与各自簇中心距离之和）不再降低，返回最后的聚类结果

下面对一个简单的小例子在Python与R中的K-modes聚类过程为例进行说明：

Python

我们使用的是第三方包kmodes中的方法，具体过程如下：

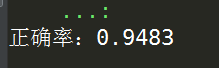
import numpy as np
from kmodes import kmodes

'''生成互相无交集的离散属性样本集'''
data1 = np.random.randint(1,6,(10000,10))
data2 = np.random.randint(6,12,(10000,10))

data = np.concatenate((data1,data2))

'''进行K-modes聚类'''
km = kmodes.KModes(n_clusters=2)
clusters = km.fit_predict(data)

'''计算正确归类率'''
score = np.sum(clusters[:int(len(clusters)/2)])+(len(clusters)/2-np.sum(clusters[int(len(clusters)/2):]))
score = score/len(clusters)
if score >= 0.5:
    print('正确率：'+ str(score))
else:
    print('正确率：'+ str(1-score))

R

在R中进行K-modes聚类的包为klaR，用其中的kmodes(data,modes=k)进行聚类，其中modes为指定的类数目k，具体示例如下：

> library(klaR)
> 
> data1 <- matrix(sample(1:3,size=1000,replace = T),nrow=100)
> data2 <- matrix(sample(4:6,size=1000,replace = T),nrow=100)
> data <- rbind(data1,data2)
> 
> km <- kmodes(data, modes=2)
> s <- km$cluster
> if(mean(s[1:100] < 1.5)){
+   score <- sum(s[1:100])+sum(s[101:200]-1)
+   score <- score/200
+   cat('正确率：',score)
+ }else{
+   score <- sum(s[1:100]-1)+sum(s[101:200])
+   score <- score/200
+   cat('正确率：',round(score,3))
+ }
正确率： 0.995

以上便是关于K-modes聚类的简要介绍，如有错误望指出。