DBSCAN算法是一种很典型的密度聚类法,它与K-means等只能对凸样本集进行聚类的算法不同,它也可以处理非凸集。
关于DBSCAN算法的原理,笔者觉得下面这篇写的甚是清楚练达,推荐大家阅读:
https://www.cnblogs.com/pinard/p/6208966.html
DBSCAN的主要优点有:
1) 可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
2) 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
3) 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN的主要缺点有:
1)如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
2) 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3) 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
R中的fpc包中封装了dbscan(data,eps,MinPts),其中data为待聚类的数据集,eps为距离阈值ϵ,MinPts为样本数阈值,这三个是必须设置的参数,无缺省项。
一、三种聚类算法在非凸样本集上的性能表现
下面我们以正弦函数为材料构造非凸样本集,分别使用DBSCAN、K-means、K-medoids算法进行聚类,并绘制最终的聚类效果图:
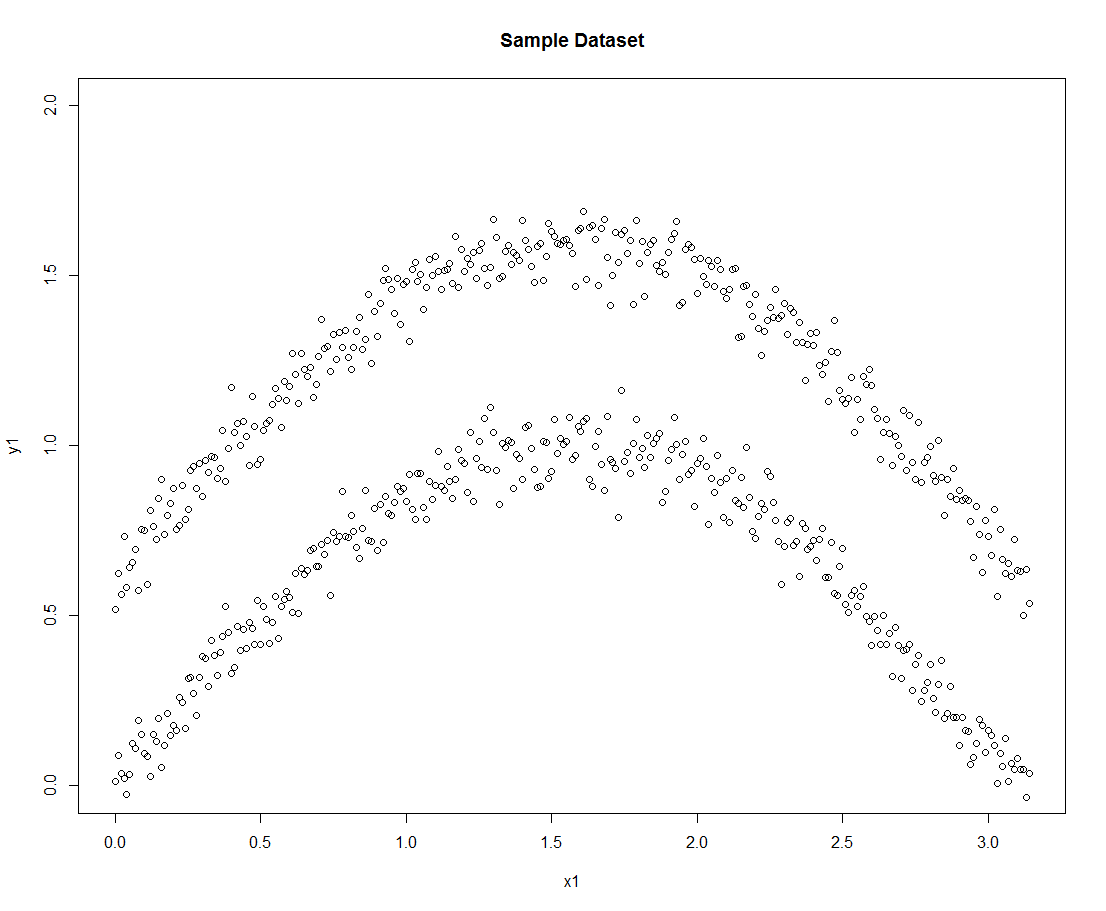
library(fpc) library(cluster) #构造非凸样本集 x1 <- seq(0,pi,0.01) y1 <- sin(x1)+0.06*rnorm(length(x1)) y2 <- sin(x1)+0.06*rnorm(length(x1))+0.6 plot(x1,y1,ylim=c(0,2.0)) points(x1,y2) c1 <- c(x1,x1) c2 <- c(y1,y2) data1 <- as.matrix(cbind(c1,c2))
构造的样本集如下:
接着我们依次使用上述三种聚类算法:
#分别绘制三种聚类算法的聚类效果图 par(mfrow=c(1,3)) #DBSCAN聚类法 db <- dbscan(data1,eps=0.2,MinPts = 5) db$cluster plot(data1,col=db$cluster) title('DBSCAN Cluster') #K-means聚类法 km <- kmeans(data1,centers=2) km$cluster plot(data1,col=km$cluster) title('K-means Cluster') #K-medoids聚类法 pm <- pam(data1,k=2) pm$clustering plot(data1,col=pm$clustering) title('K-medoids Cluster')
具体的聚类效果如下:
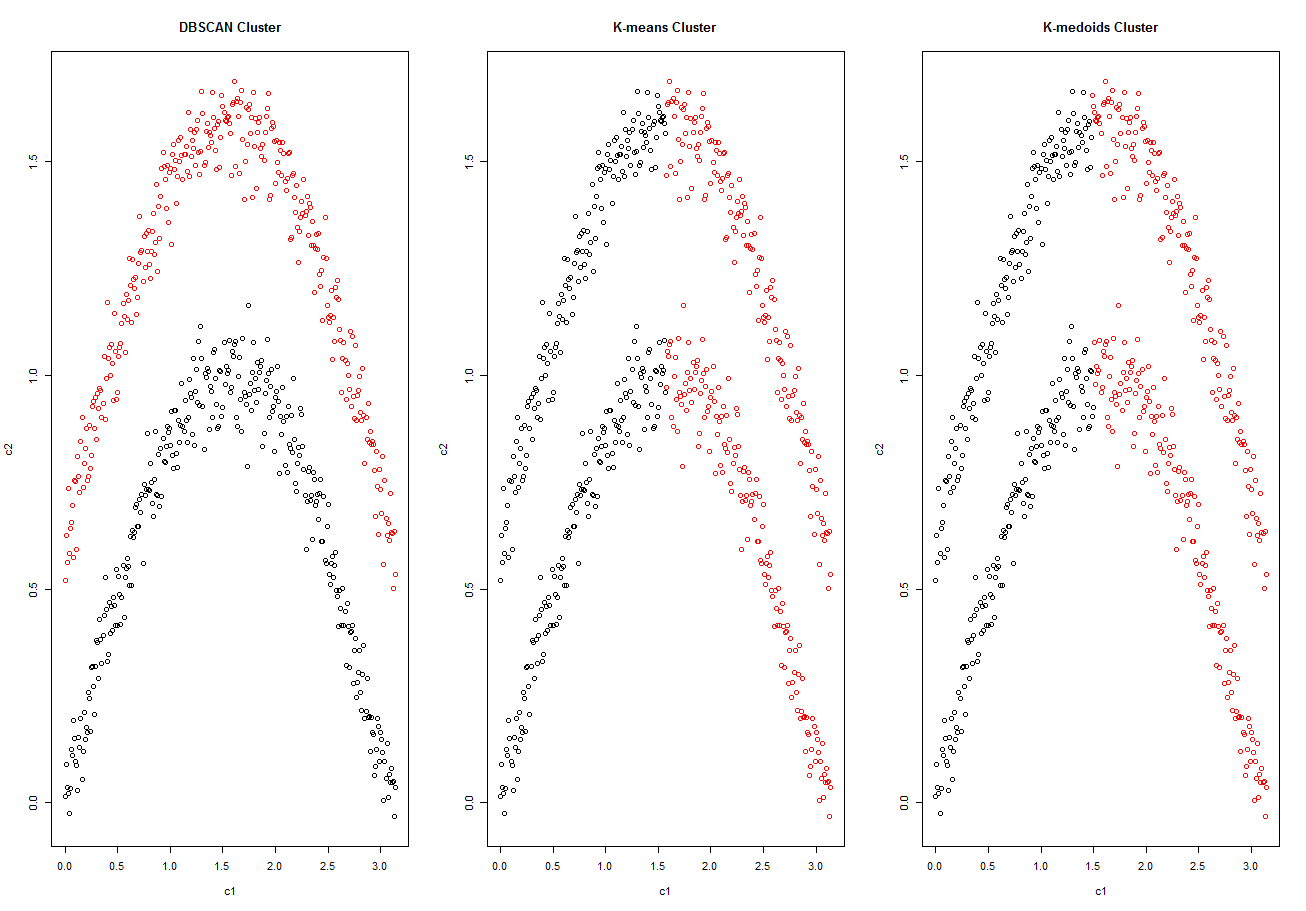
可以看出,在对非凸样本集的聚类上,DBSCAN效果非常好,而另外两种专门处理凸集的聚类算法就遇到了麻烦。
二、DBSCAN算法在常规凸样本集上的表现
上面我们研究了DBSCAN算法在非凸样本集上的表现,比K-means和K-medoids明显优秀很多,下面我们构造一个10维的凸样本集,具体的代码和聚类结果如下:
> library(fpc) > library(Rtsne) > > #创建待聚类数据集 > data1 <- matrix(rnorm(10000,0,0.6),nrow=1000) > data2 <- matrix(rnorm(10000,1,0.6),nrow=1000) > > data <- rbind(data1,data2) > > #对原高维数据集进行降维 > tsne <- Rtsne(data) > > par(mfrow=c(4,4)) > for(i in 1:16){ + #进行DBSCAN聚类 + db <- dbscan(data,eps=1.1+i*0.025,MinPts = 25) + #绘制聚类效果图 + plot(tsne$Y[,1],tsne$Y[,2],col=db$cluster) + title(paste('eps=',as.character(1.1+i*0.025),sep='')) + print(paste('eps=',as.character(1.1+i*0.025))) + print(table(db$cluster)) + } [1] "eps= 1.125" 0 2000 [1] "eps= 1.15" 0 1 2 1950 26 24 [1] "eps= 1.175" 0 1 2 1920 59 21 [1] "eps= 1.2" 0 1 2 1834 120 46 [1] "eps= 1.225" 0 1 2 1682 177 141 [1] "eps= 1.25" 0 1 2 1515 250 235 [1] "eps= 1.275" 0 1 2 1305 344 351 [1] "eps= 1.3" 0 1 2 1163 425 412 [1] "eps= 1.325" 0 1 2 989 521 490 [1] "eps= 1.35" 0 1 2 854 596 550 [1] "eps= 1.375" 0 1 2 707 670 623 [1] "eps= 1.4" 0 1 2 572 732 696 [1] "eps= 1.425" 0 1 2 500 766 734 [1] "eps= 1.45" 0 1 420 1580 [1] "eps= 1.475" 0 1 355 1645 [1] "eps= 1.5" 0 1 285 1715
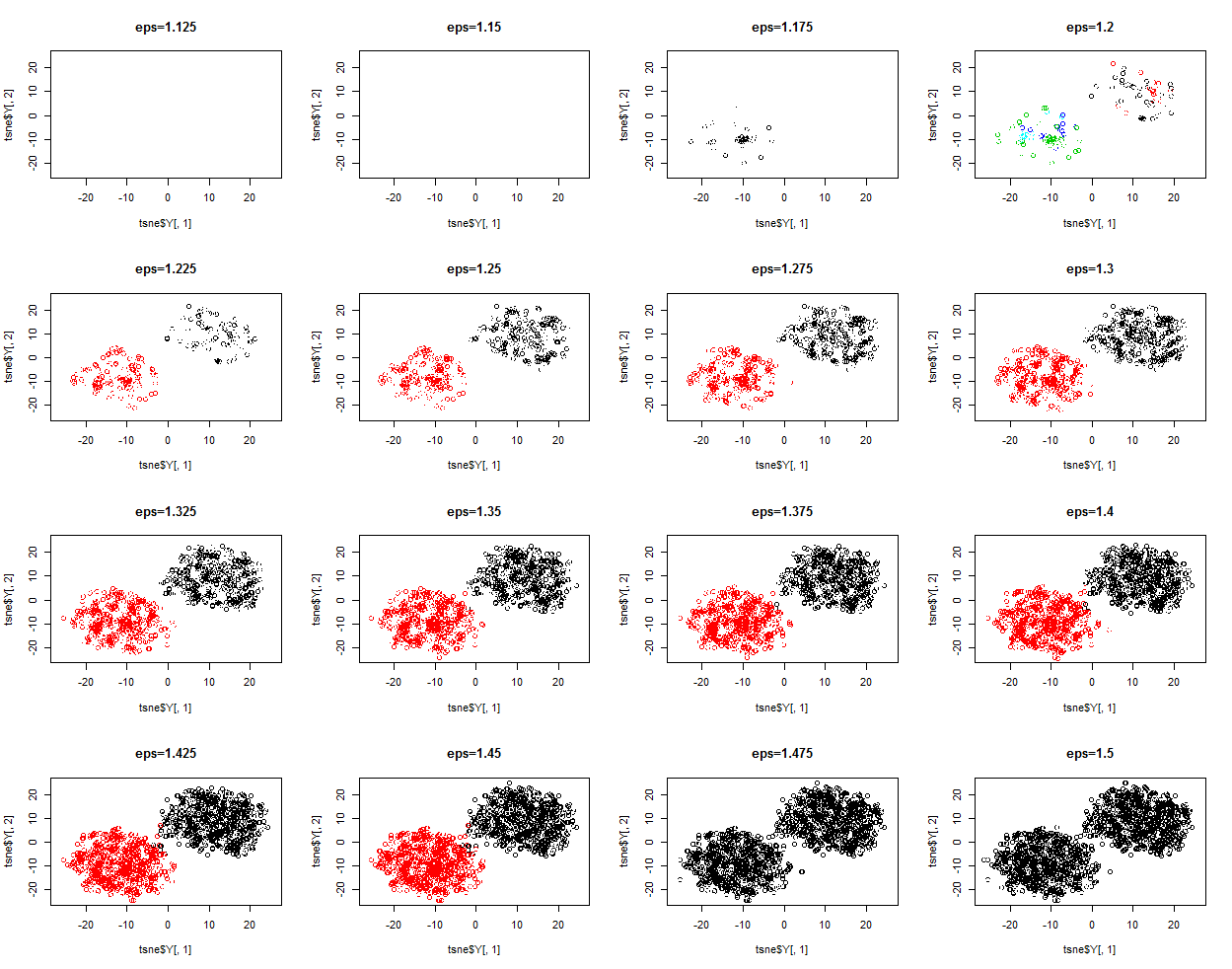
可以看出,DBSCAN虽然性能优越,但是涉及到有些麻烦的调参数的过程,需要进行很多次的试探,没有K-means和K-medoids来的方便快捷。
Python
在Python中,DBSCAN算法集成在sklearn.cluster中,我们利用datasets构造两个非凸集和一个凸集,效果如下:
from sklearn import datasets import numpy as np import matplotlib.pyplot as plt from matplotlib.pyplot import style from sklearn.cluster import KMeans,DBSCAN style.use('ggplot') '''构造样本集''' X1, y1=datasets.make_circles(n_samples=5000, factor=.6,noise=.05) X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9) X = np.concatenate((X1, X2)) plt.scatter(X[:, 0], X[:, 1], marker='*') plt.title('Samples')
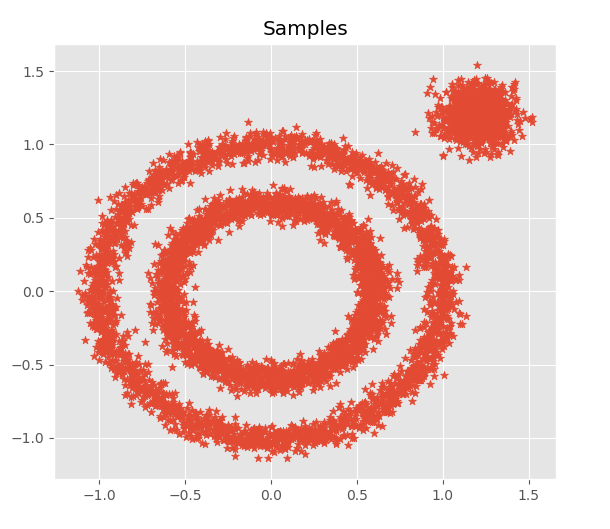
分别使用K-means和DBSCAN对上述样本集进行聚类,效果如下:
'''利用K-means''' km = KMeans(n_clusters=3).fit_predict(X) col = [(['red','green','blue','yellow','grey','purple'])[i] for i in km] plt.figure(figsize=(16,8)) plt.subplot(121) plt.scatter(X[:, 0], X[:, 1], marker='*',c=col) plt.title('K-means') '''利用DBSCAN''' db = DBSCAN(eps = 0.12, min_samples = 19).fit_predict(X) col = [(['red','green','blue','yellow'])[i] for i in db] plt.subplot(122) plt.scatter(X[:, 0], X[:, 1], marker='*',c=col) plt.title('DBSCAN')

对DBSCAN中的参数eps(超球体半径)进行试探:
'''对eps进行试探性调整''' plt.figure(figsize=(15,15)) for i in range(9): db = DBSCAN(eps = 0.05+i*0.04, min_samples = 19).fit_predict(X) col = [(['red','green','blue','yellow','purple','aliceblue','antiquewhite','black','blueviolet','cyan','darkgray'])[i] for i in db] plt.subplot(331+i) plt.scatter(X[:, 0], X[:, 1], marker='*',c=col) plt.title('eps={}'.format(str(round(0.05+i*0.04,2))))
对DBSCAN中的参数MinPts(核心点内最少样本个数)进行试探:
'''对MinPts进行试探性调整''' plt.figure(figsize=(15,15)) for i in range(9): db = DBSCAN(eps = 0.12, min_samples = 10+i*4).fit_predict(X) col = [(['red','green','blue','yellow','purple','aliceblue','antiquewhite','black','blueviolet','cyan','darkgray'])[i] for i in db] plt.subplot(331+i) plt.scatter(X[:, 0], X[:, 1], marker='*',c=col) plt.title('MinPts={}'.format(str(round(10+i*4))))

可见参数的设置对聚类效果的影响非常显著。
以上就是DBSCAN的简单介绍,若发现错误望指出。