严格来讲矩是概率与统计中的一个概念,是随机变量的一种数字特征。设 x 为随机变量,C为常数,则量E[(x−c)^k]称为X关于C点的k阶矩。比较重要的两种情况如下:
1.c=0,这时a_k=E(X^k)称为X的k阶原点矩;
2.c=E(X),这时μ_k=E[(X−EX)^k]称为X的k阶中心矩
一阶原点矩就是期望,一阶中心矩μ_1=0,二阶中心矩μ_2就是X的方差Var(X)。在统计学上,高于4阶的矩极少使用,μ_3可以去衡量分布是否有偏,μ_4可以衡量分布(密度)在均值拘谨的陡峭程度。
对于数学来说

矩、中心矩、质心、patch方向
一阶原点矩就是期望。二阶中心矩就是随机变量的的方差. 在统计学上,高于4阶的矩极少使用。三阶中心距可以去衡量分布是否有偏。四阶中心矩可以去衡量分布在均值附近的陡峭程度如何。
那针对一幅图像,我们把像素的坐标看成是一个二维随机变量(X, Y),那么一副灰度图可以用二维灰度图密度函数来表示,因此可以用矩来描述灰度图像的特征。

空间矩的实质为面积或者质量。可以通过一阶矩计算质心/重心。
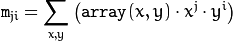
重心(中心centers):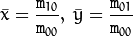
Hu矩




class Moments{ public: Moments(); Moments(double m00, double m10, double m01, double m20, double m11, double m02, double m30, double m21, double m12, double m03 ); Moments( const CvMoments& moments ); operator CvMoments() const; // spatial moments 空间矩 double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03; // central moments 中心矩 double mu20, mu11, mu02, mu30, mu21, mu12, mu03; // central normalized moments 中心归一化矩 double nu20, nu11, nu02, nu30, nu21, nu12, nu03; }

#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
using namespace cv;
using namespace std;
//定义窗口名字的宏
#define WINDOW_NAME1 "【原始图】"
#define WINDOW_NAME2 "【图像轮廓】"
//全局变量的声明
Mat g_srcImage, g_grayImage;
int g_nThresh = 100;
int g_nMaxThresh = 255;
RNG g_rng(12345);
Mat g_cannyMat_output;
vector<vector<Point> > g_vContours;
vector<Vec4i>g_vHierarchy;
//全局函数声明
void on_ThreshChange(int, void*);
//main()函数
int main()
{
//改变console字体颜色
system("color 1E");
//读入原图,返回3通道图像数据
g_srcImage = imread("E:\VS2015Opencv\vs2015\project\picture\01.jpg", 1);
//源图像转化为灰度图像并平滑
cvtColor(g_srcImage, g_grayImage, COLOR_BGR2GRAY);
blur(g_grayImage, g_grayImage, Size(3, 3));
//创建新窗口
namedWindow(WINDOW_NAME1, WINDOW_AUTOSIZE);
imshow(WINDOW_NAME1, g_srcImage);
//创建滚动条并进行初始化
createTrackbar("阈值:", WINDOW_NAME1, &g_nThresh, g_nMaxThresh, on_ThreshChange);
on_ThreshChange(0, 0);
waitKey(0);
return 0;
}
void on_ThreshChange(int, void *)
{
//使用canny检测边缘
Canny(g_grayImage, g_cannyMat_output, g_nThresh, g_nThresh * 2, 3);
//找到轮廓
findContours(g_cannyMat_output, g_vContours, g_vHierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));
//计算矩
vector<Moments> mu(g_vContours.size());
for (unsigned int i = 0; i < g_vContours.size(); i++)
{
mu[i] = moments(g_vContours[i], false);
}
//计算中心矩
vector<Point2f>mc(g_vContours.size());
for (unsigned int i = 0; i < g_vContours.size(); i++)
{
mc[i] = Point2f(static_cast<float>(mu[i].m10 / mu[i].m00), static_cast<float>(mu[i].m01 / mu[i].m00));
}
//绘制轮廓
Mat drawing = Mat::zeros(g_cannyMat_output.size(), CV_8UC3);
for (unsigned int i = 0; i < g_vContours.size(); i++)
{
//随机生成颜色值
Scalar color = Scalar(g_rng.uniform(0, 255), g_rng.uniform(0, 255), g_rng.uniform(0, 255));
//绘制外层和内层轮廓
drawContours(drawing, g_vContours, i, color, 2, 8, g_vHierarchy, 0, Point());
//绘制圆
circle(drawing, mc[i], 4, color, -1, 8, 0);
}
//显示到窗口中
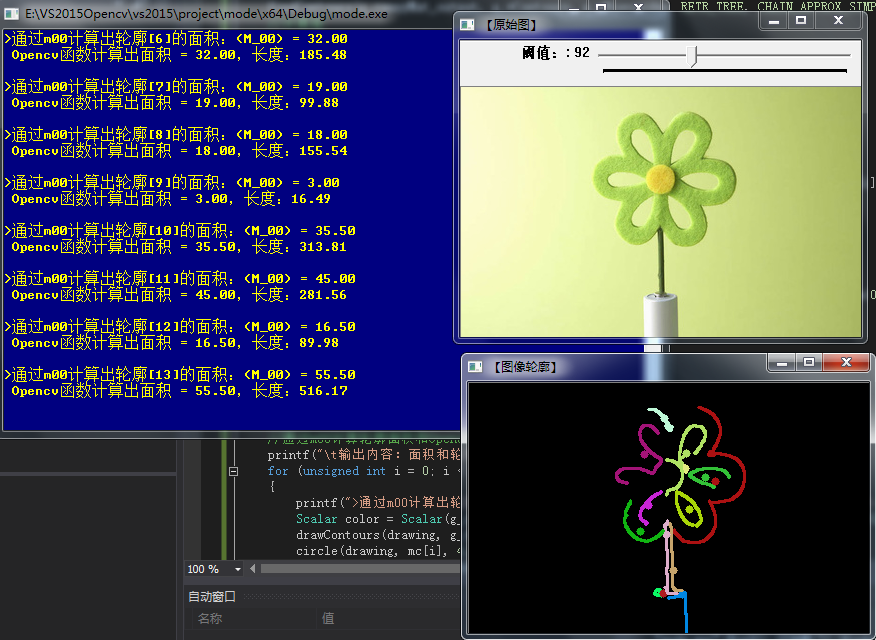
namedWindow(WINDOW_NAME2, WINDOW_AUTOSIZE);
imshow(WINDOW_NAME2, drawing);
//通过m00计算轮廓面积和Opencv函数比较
printf(" 输出内容:面积和轮廓长度
");
for (unsigned int i = 0; i < g_vContours.size(); i++)
{
printf(">通过m00计算出轮廓[%d]的面积:(M_00) = %.2f
Opencv函数计算出面积 = %.2f,长度:%.2f
", i, mu[i].m00, contourArea(g_vContours[i]), arcLength(g_vContours[i], true));
Scalar color = Scalar(g_rng.uniform(0, 255), g_rng.uniform(0, 255), g_rng.uniform(0, 255));
drawContours(drawing, g_vContours, i, color, 2, 8, g_vHierarchy, 0, Point());
circle(drawing, mc[i], 4, color, -1, 8, 0);
}
}
本文参考:图像的形状特征——图像的矩