14java的冒泡排序

冒泡排序

以前学习C语言的时候学习过冒泡排序等其他排序，现在根据自己对冒泡的回忆以及理解先分析一下冒泡排序的原理 :

主要是理解“冒泡”二字，每冒一个泡就把数组内的元素遍历一次，调整一个数字的位置（如果顺序不对的话），一共需要进行array.length-1次遍历，每次遍历需要进行array.length-i-1次比较（其中i是指第i次遍历）。图1 是第一次遍历的过程，红字是比较的两个数字，根据比较决定是否需要调整次序。下一轮依次类推。

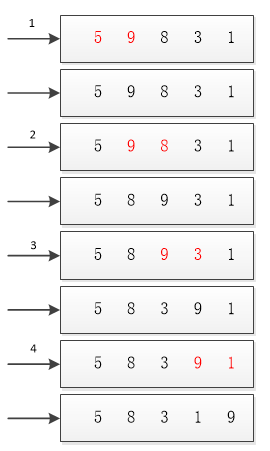
图1

package Demoxx;

import MethodDemo.Demo08;

public class Demo01 {
    public static void main(String[] args) {
        int[] array = {5,9,8,3,1,5,7,3,6};//长度为9
        System.out.println("Sort before:");
        Demo08 demo08 = new Demo08();
        demo08.PrintArray(array);
        //冒泡排序，升序
        int temp=0;
        for (int i = 0; i < array.length; i++) {
            for (int j = array.length-1; j >0 ; j--) {
                if (array[j] < array[j - 1]) {
                    temp = array[j - 1];
                    array[j - 1] = array[j];
                    array[j]=temp;
                }
            }
        }
        System.out.println("Sort after:");
        demo08.PrintArray(array);
    }
}

这个排序也能正确进行排序输出，但是注意到一点，这里的每次遍历时都进行了array.length-1次数组元素的比较，思考一下，我们正在进行升序排序，上一轮已经把最大的一个元素放在了数组的最后一个索引位置，那么下一次遍历就不需要再和最后一个元素进行比较了，因为它就是最大的。

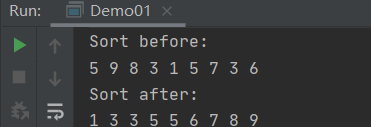
​ 图2

下面是改进的冒泡排序程序

package Demoxx;

import MethodDemo.Demo08;

import java.util.Arrays;

public class Demo01 {
    public static void main(String[] args) {
        //冒泡排序,升序
        int[] array = {5, 9, 8, 3, 1, 5, 7, 3, 6};//长度为9
        System.out.println("Sort before:");
        Demo08 demo08 = new Demo08();
        demo08.PrintArray(array);
        int[] array_sort = sortArray(array);
        System.out.println("Sort after:");
//        demo08.PrintArray(array);//调用自写的方法输出
        System.out.println(Arrays.toString(array_sort));//复习一下这个用法

    }

    public static int[] sortArray(int[] array) {//特别注意这里的返回值类型，int型数组需要加上[]
        int temp = 0;
        for (int i = 0; i < array.length - 1; i++) {
            for (int j = 0; j < array.length - i - 1; j++) {
                if (array[j] > array[j + 1]) {
                    temp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = temp;
                }
            }
        }
        return array;//注意这里和写方法处的配合，这里不用加[]
    }
}

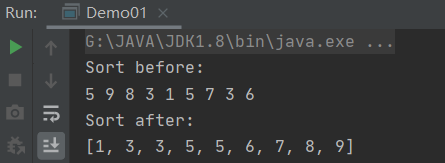
冒泡排序的时间复杂度：

假如一维数组的长度是n，在最坏的情况下（需要调整所有的元素的顺序）需要进行n*(n-1)次调整，那么他的时间复杂度是O(n^2)

还有多种排序算法，如：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

算法的时间复杂度:

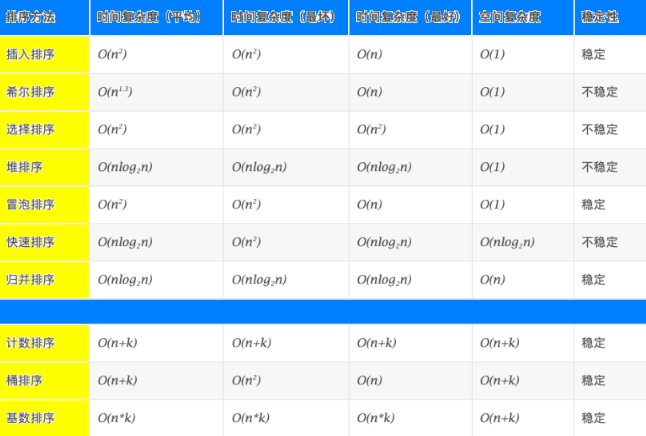
• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
• 时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机

内执行时所需存储空间的度量，它也是数据规模n的函数。