解释题面:
给你一棵树,每个点上有权值(0或1),问通过更改点权(1变0或0变1)达到相似的指定状态最少需要多少次。
相似状态的定义为“看起来是一样的”,就是说不一定每个点都是和原来的位置对应的,只要树的形状没变,树(包括点权)与目标树同构即可。
比如:下面这两棵树就是“看起来一样的”
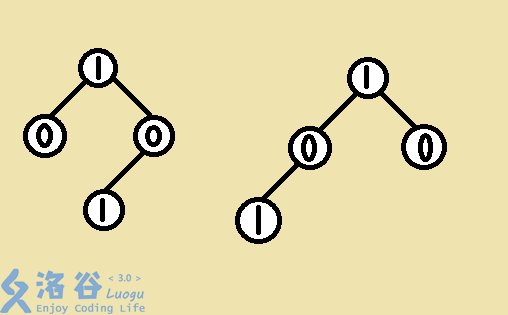
首先固定一棵树,枚举另一棵树,显然另一棵树只有与固定的树同构才有可能产生贡献。
如果固定的树以重心为根,那么另一棵树最多就只有重心为根才有可能同构了(可能有两个)。
然后就是求改动次数最小值,设(f[x][y])表示以第一棵树(x)为根的子树内和第二棵树(y)为根的子树内,达到目标最少需要改动的次数
我们发现只有同构的子树需要决策,我们把同构的子树分别拿出来,我们要做的就是做一个匹配,跑一边KM或者费用流就好了
(f[x][y])要记忆化一下,判断同构用树哈希即可
#define B cout << "BreakPoint" << endl;
#define O(x) cout << #x << " " << x << endl;
#define O_(x) cout << #x << " " << x << " ";
#define Msz(x) cout << "Sizeof " << #x << " " << sizeof(x)/1024/1024 << " MB" << endl;
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#include<set>
#define pb push_back
#define LL long long
const int inf = 1e9 + 9;
using namespace std;
inline int read() {
int s = 0,w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-')
w = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = s * 10 + ch - '0';
ch = getchar();
}
return s * w;
}
const int N = 1410,bas = 10007;
int n,head[N],nxt[N * 2],to[N * 2],cnt,sz[N],fa[N] = {N},rt,a[N],b[N];
LL v[N];
vector<int>v1[N],v2[N];
void add(int x,int y){
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void getroot(int x,int last){
sz[x] = 1,fa[x] = 0;
for(int i = head[x];i;i = nxt[i]){
int u = to[i];
if(u == last)continue;
getroot(u,x);
sz[x] += sz[u];
fa[x] = max(fa[x],sz[u]);
}
fa[x] = max(fa[x],n - sz[x]);
if(fa[x] < fa[rt]) rt = x;
}
bool comp(const int &i,const int &j){ return v[i] < v[j];}
void dfs(int x,int last,vector<int>*V){
sz[x] = 1,v[x] = 0;
vector<int>().swap(V[x]);
for(int i = head[x];i;i = nxt[i]){
int u = to[i];
if(u == last)continue;
dfs(u,x,V);
sz[x] += sz[u];
V[x].pb(u);
}
sort(V[x].begin(),V[x].end(),comp);
for(int i = V[x].size() - 1;i >= 0;i--) v[x] = v[x] * N + v[V[x][i]];
v[x] = v[x] * N + sz[x];
}
int f[N][N],c[N][N];
namespace sks{
int head[N],nxt[N * 8],to[N * 8],tot = 1,c[N * 8],dis[N * 8],S,T,ans = 0,f[N],pre[N];
queue<int>Q;
bool vis[N];
void add(int x,int y,int z,int co){
to[++tot] = y,nxt[tot] = head[x],head[x] = tot,dis[tot] = z,c[tot] = co;
to[++tot] = x,nxt[tot] = head[y],head[y] = tot,dis[tot] = 0,c[tot] = -co;
}
void init(){
for(int i = S;i <= T;i++) head[i] = 0;
tot = 1,ans = 0;
}
bool spfa(){
for(int i = S;i <= T;i++) f[i] = N,vis[i] = 0;
Q.push(S);
vis[S] = 1;f[S] = 0;
while(!Q.empty()){
int x = Q.front();
Q.pop();
for(int i = head[x];i;i = nxt[i]){
if(dis[i] <= 0)continue;
int u = to[i];
if(f[x] + c[i] < f[u]){
f[u] = f[x] + c[i],pre[u] = i;
if(!vis[u]) Q.push(u),vis[u] = 1;
}
}
vis[x] = 0;
}
if(f[T] == N) return false;
int x = T;
ans += f[T];
while(x) dis[pre[x]]--,dis[pre[x] ^ 1]++,x = to[pre[x] ^ 1];
return true;
}
}
int solve(int n){
sks::init();
sks::S = 0;sks::T = n + n + 1;
for(int i = 1;i <= n;i++){
sks::add(sks::S,i,1,0);sks::add(i + n,sks::T,1,0);
for(int j = 1;j <= n;j++) sks::add(i,j + n,1,c[i][j]);
}
while(sks::spfa());
return sks::ans;
}
int sec(int x,int y){
if(f[x][y] != -1) return f[x][y];
f[x][y] = b[y] ^ a[x];
for(int i = 0,li = v1[x].size() - 1;i <= li;i++){
int j = i;
while(j < li && v[v1[x][j + 1]] ==v [v1[x][i]]) j++;
for(int k = i;k <= j;k++) for(int l = i;l <= j;l++) sec(v1[x][k],v2[y][l]);
for(int k = i;k <= j;k++) for(int l = i;l <= j;l++) c[k - i + 1][l - i + 1] = sec(v1[x][k],v2[y][l]);
f[x][y] += solve(j - i + 1);
i = j;
}
return f[x][y];
}
int main(){
n = read();
int ans = inf;
for(int i = 2;i <= n;i++){
int x = read(),y = read();
add(x,y),add(y,x);
}
for(int i = 1;i <= n;i++) a[i] = read();
for(int i = 1;i <= n;i++) b[i] = read();
getroot(1,1);
dfs(rt,rt,v2);
LL tmp = v[rt];
for(int i = 1;i <= n;i++){
dfs(i,i,v1);
if(v[i] == tmp){
memset(f,-1,sizeof(f));
ans = min(ans,sec(i,rt));
}
}
printf("%d
",ans);
return 0;
}