要实现归并排序递归方法:
第一步:先将原来的数据表分成排好序的子表,然后调用合并函数对子表进行归并,使之成为有序表
例如有如下向量:
⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽ ⑾
25, 10, 7, 19, 3, 48, 12, 17, 56, 30, 21
/
25,10,7,19,3 48,12,17,56,30,21
/ /
25,10 7,19,3 48,12,17 56,30,21
/ / / /
25 10 7 19,3 ... ... ... ...
归并算法划分子表和归并子表与原数据序列次序无关,因此算法最坏情况,最坏情况和平均情况时间复杂度是一样的,时间复杂度为O(NlogN),空间复杂度O(N+logN)
#include <stdio.h>
#include <stdlib.h>
void Merge(int arr[], int beg, int mid, int end)
{
int i = beg;
int j = mid + 1;
int p = 0;
int *ipa;
ipa = (int*)malloc((end-beg+1) * sizeof(int));
if(!ipa) return;
while(i <= mid && j <= end)
{
//ipa[p++] = (arr[i]<=arr[j])?arr[i++]:arr[j++];
if(arr[i] <= arr[j])
{
ipa[p] = arr[i];
p++;
i++;
}
else
{
ipa[p] = arr[j];
p++;
j++;
}
}
while(i<=mid)
{
ipa[p++] = arr[i++];
}
while(j<=end)
{
ipa[p++] = arr[j++];
}
for(p=0, i=beg; i<=end; p++, i++)
{
arr[i] = ipa[p];
}
free(ipa);
}
void MergeSort(int arr[], int beg, int end)
{
int mid;
if(beg < end)
{
mid = (beg + end)/2;
MergeSort(arr, beg, mid);
MergeSort(arr, mid+1, end);
Merge(arr, beg, mid, end);
}
}
int main()
{
int a[9] = {7,10,48,25,12,17,21,48,30};
printf("Before Merge Sort:
");
for(int i=0; i<9; i++)
{
printf("%d ", a[i]);
}
printf("
");
printf("After Merge Sort:
");
MergeSort(a, 0, 8);
for(int i=0; i<9; i++)
{
printf("%d ", a[i]);
}
printf("
");
return 0;
}
这是一个递归算法,这个算法的理解其实可以借助下面这个图:
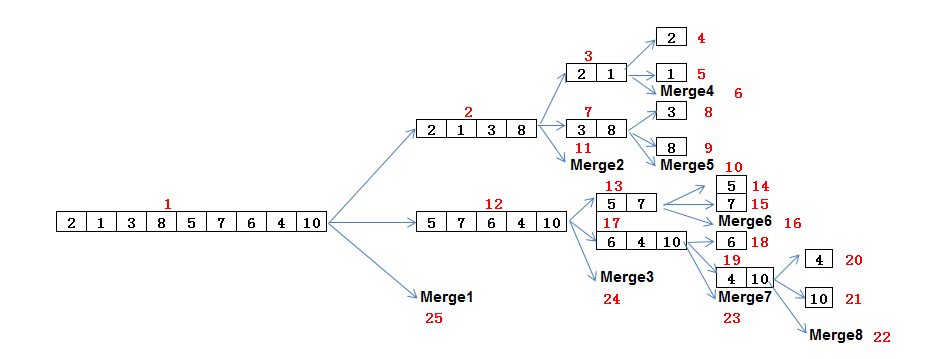
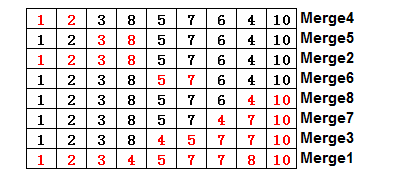
对于原始的数组2,1,3,8,5,7,6,4,10,在整个过程执行的是顺序是途中红色编号1-20。虽然我们描述中说的是程序先分解,再归并,但实际过程是一边分解一边归并,前半部分分先排好序,后半部分再拍好,最后整个归并为一个完整的序列,途中的merge过程它所在层的两个序列的merge过程:下图展示了每个merge过程对作用于数组的哪部分(红色)。
整个过程就像一个动态的树,执行顺序就是对树的先序遍历顺序。