简述
快速排序的基本思想是分治,这一点与归并排序一样。实现原理是选择一个元素作为中轴,根据与中轴的关系进行分组(比中轴大的放一起,比中轴小的放一起),分组后的元素在分别进行相同的操作,直到无法再进行分组,最后得到便是有序的数组。
分类
分类依据:主要由如何选取选择中轴引起的分类
常见分类:
- 始终选择数组的第一个元素为中轴
- 始终选择数组的最后一个元素为中轴(代码示例采用的方式)
- 随机选择元素最为中轴
- 选择首位元素、中间元素和末尾元素的中位数最为中轴
无论采取何种分类方式,仅仅是中轴的选择不同(效率也不同),但是其基本原理是一样的。
代码
package test;
public class QuickSort {
public static int partition(int[] arr, int low,int high){
//使用数组最后一个元素作为中轴
int pivot = arr[high];
//初始化i
int i = (low-1);
//循环数组
for(int j=low; j<high; j++){
//如果j对应的元素比中轴元素小
if(arr[j] < pivot){
i++;
//交换i和j对应的元素
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//将中轴元素交换的i+1的位置
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
//返回中轴元素对应的索引
return i+1;
}
public static void sort(int[] arr,int low,int high){
if(low < high){
//返回分组的索引
int pi = partition(arr, low, high);
//递归排序前半部分
sort(arr, low, pi - 1);
//递归排序后半部分
sort(arr, pi + 1, high);
}
}
public static void main(final String[] args) {
int[] arr = {2,4,3,9,5,3,8,7,6};
sort(arr, 0, arr.length-1);
for (int i : arr) {
System.out.print(i + " ");
}
}
}
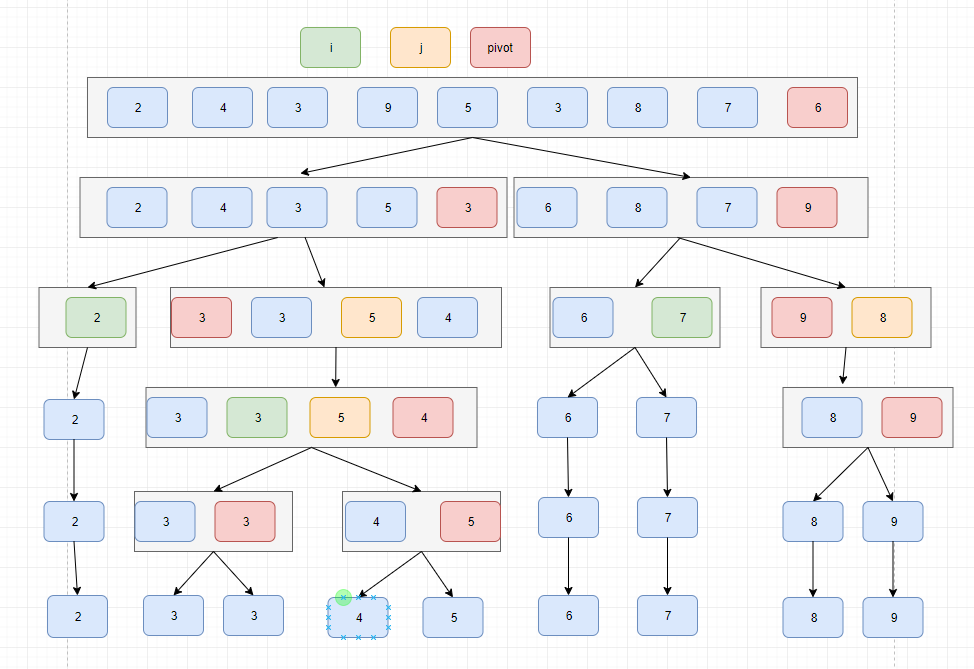
图解
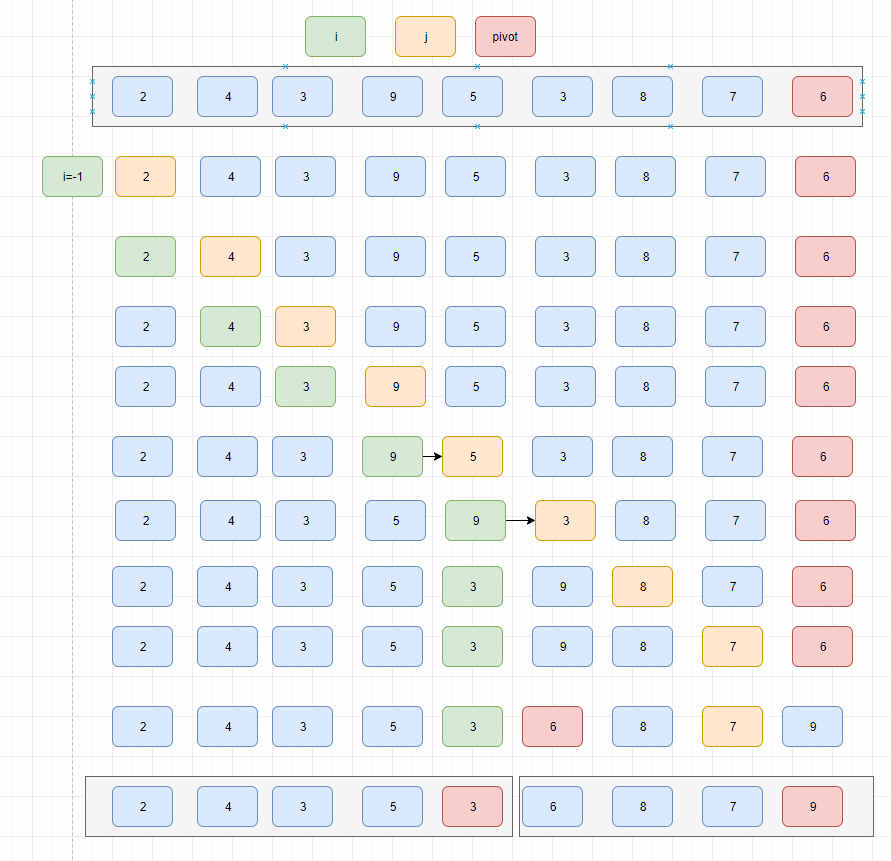
2.(注意此处的两个3)
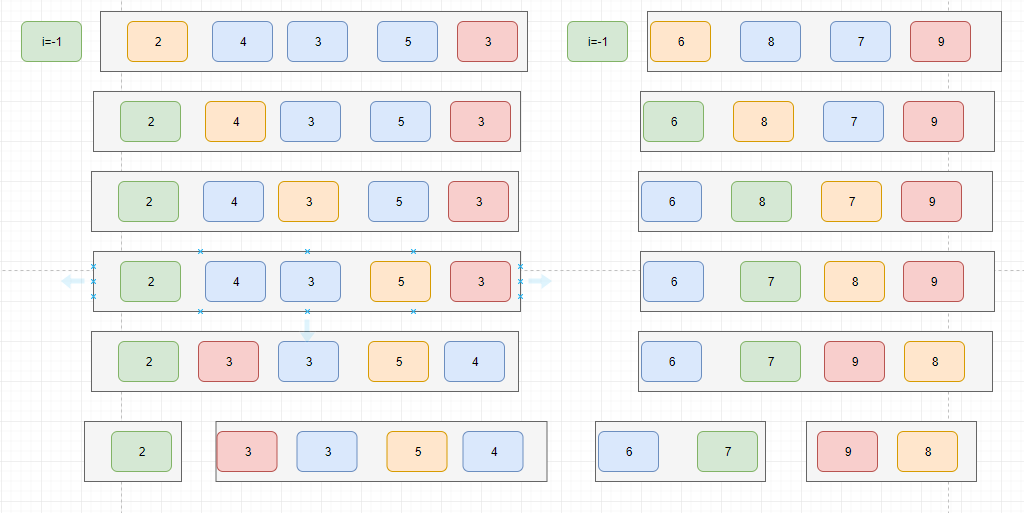
3.完成
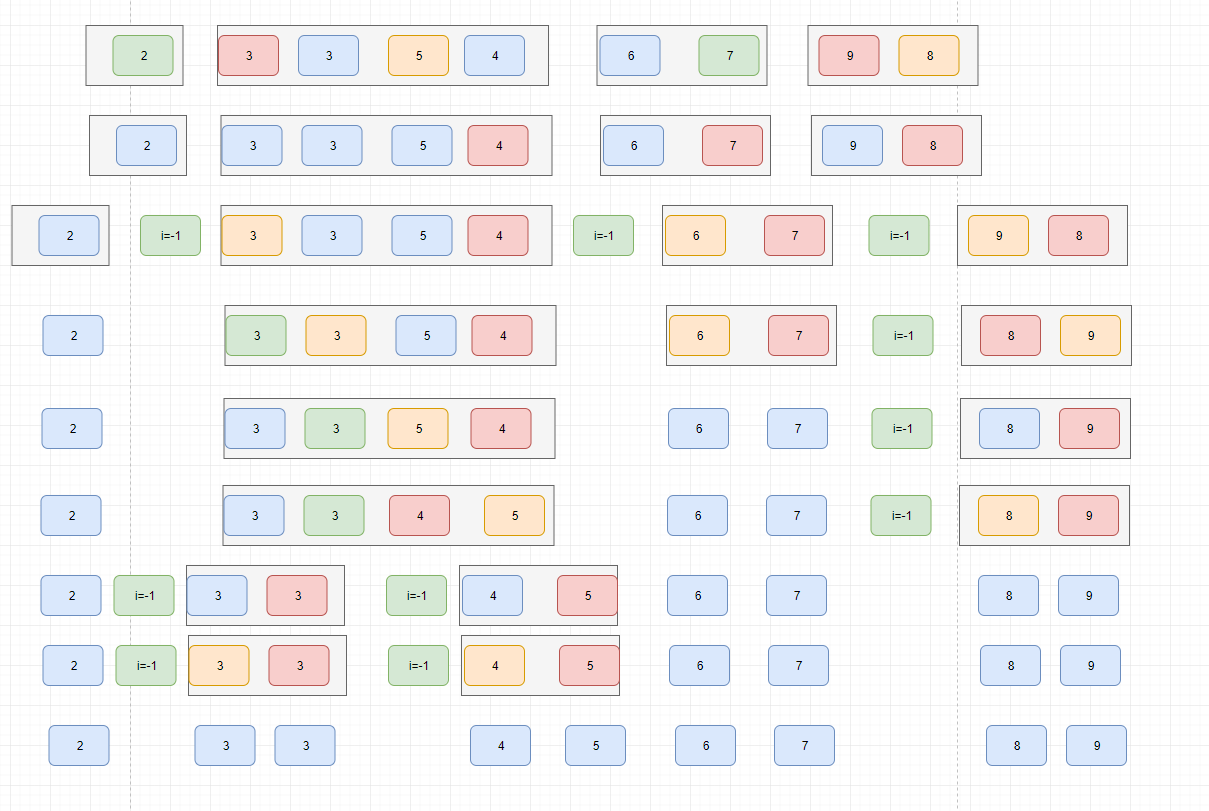
4.总览
算法分析
- 时间复杂度
最优:分组过程中始终都是选择中间元素--O(nlong n)
最差:每次分组选的中轴元素始终都是最大值或者是最小值--O(n^2)
平均:O(nlog n)
- 稳定性:图解使用的实现方式不稳定(图解实例2中的3)
3分法简述
基本原理一样,但是在分组时划分如下:
- 大于中轴元素的
- 等于中轴元素的
- 小于中轴元素的
此种方式在冗余元素比较多的情况下速度较快
例如:[1,3,4,4,3,3,3,3,4,2,1,3,2,2,4]