又是线段树（维护方差）

我们把方差公式展开

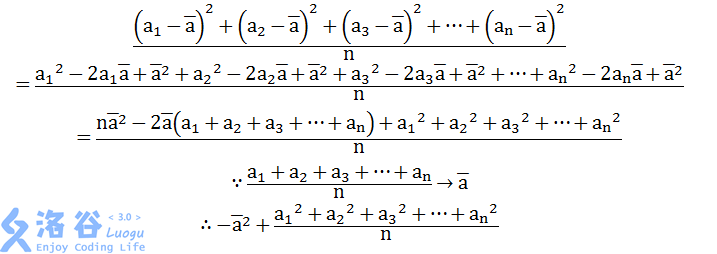
所以只需要维护一个区间平方和和区间和

当我们更新一个区间加时

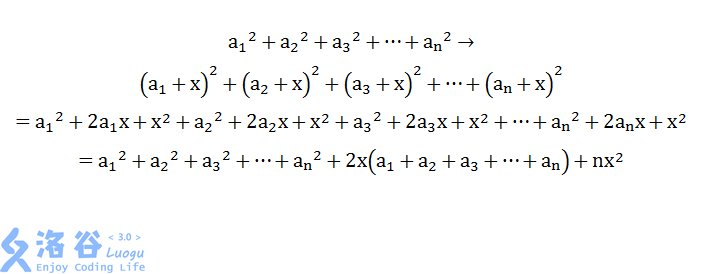
所以pushdown就很好写了

具体见代码

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cmath>
#define int long long
using namespace std;
#define ls(x) (x<<1)
#define rs(x) (ls(x)|1)
const int maxn=5e5+5;
struct FFF{
    int l,r;
    double sum;
	double sqr;
    double add;
    int mid(){return l+r>>1;}
    int len(){return r-l+1;}
	FFF(){l=r=0;sum=sqr=add=0;}
}t[maxn<<2];
int n,m;
void build(int l=1,int r=n,int o=1){
    t[o].l=l;t[o].r=r;
    t[o].add=0;
    if(l==r){
        scanf("%lf",&t[o].sum);
		t[o].sqr=pow(t[o].sum,2);
        return;
    }
    int mid=l+r>>1;
    build(l,mid,ls(o));
    build(mid+1,r,rs(o));
    t[o].sum=(t[ls(o)].sum+t[rs(o)].sum);
	t[o].sqr=(t[ls(o)].sqr+t[rs(o)].sqr);
}
void down(int o){
    double &v=t[o].add;
    for(int i=0;i<=1;++i){
	   t[ls(o)|i].sqr+=2*v*t[ls(o)|i].sum+t[ls(o)|i].len()*pow(v,2);
       t[ls(o)|i].sum+=t[ls(o)|i].len()*v;
	   t[ls(o)|i].add+=v;
    }
    v=0;
}
void add(int l,int r,double v,int o=1){
    if(l<=t[o].l&&t[o].r<=r){
		t[o].sqr+=2*v*t[o].sum+t[o].len()*pow(v,2);
		t[o].sum+=t[o].len()*v;
	   	t[o].add+=v;
        return;
    }
    int mid=t[o].mid();
    down(o);
    if(l<=mid)add(l,r,v,ls(o));
    if(r>mid)add(l,r,v,rs(o));
    t[o].sum=(t[ls(o)].sum+t[rs(o)].sum);
	t[o].sqr=(t[ls(o)].sqr+t[rs(o)].sqr);
}
double getsum(int l,int r,int o=1){
    if(l<=t[o].l&&t[o].r<=r){
        return t[o].sum;
    }
    double ans=0;
    int mid=t[o].mid();
    down(o);
    if(l<=mid)ans+=getsum(l,r,ls(o));
    if(r>mid)ans+=getsum(l,r,rs(o));
    return ans;
}
double getsqr(int l,int r,int o=1){
	if(l<=t[o].l&&t[o].r<=r){
        return t[o].sqr;
    }
    double ans=0;
    int mid=t[o].mid();
    down(o);
    if(l<=mid)ans+=getsqr(l,r,ls(o));
    if(r>mid)ans+=getsqr(l,r,rs(o));
    return ans;
}
signed main()
{
    cin>>n>>m;
    build();
    while(m--){
        int op,l,r;
		cin>>op>>l>>r;
		if(r<l)swap(l,r);
        if(op==1){
			double x;
			scanf("%lf",&x);
			add(l,r,x);
		}
		if(op==2){
			double sum=(double)getsum(l,r);
			printf("%.4lf
",sum/(r-l+1));
		}
		if(op==3){
			double sum=(double)getsum(l,r);
			double sqr=(double)getsqr(l,r);
			double len=(double)r-l+1;
			printf("%.4lf
",(-pow(sum/len,2)+(sqr)/len));
		}
    }
    return 0;
}