// 快速排序
/*
思路
在数组中找一个基准数(假设以数组第一个元素当基准)
将比基准数大的放到右边,比基准数小的放到他左边,最后数组一分为二,左边都比这个数大,右边都比这个数小
然后在这两个数组中再分别去操作
具体操作是将第一个元素设为基准数,从右边最后一个元素开始找,找小于等于基准数的,停下来,然后从左边第一个元素开始找,
找大于等于基准数的,停下来,然后进行交换,直到右边的和左边的指向同一个数,然后将这个数与基准数交换,此时这个数左边都比基准数大,
右边都比基准数小。
为什么要从右边开始找? 因为找到后要进行交换,从右边找到更小的,与基准交换后能确定更小的在左边更大的在右边
时间复杂度
最坏情况:
假设数组 [1,2,3,4,5] 这样一个有序的数组,基准数是1,
一开始从右边找小于等于1的,找到1本身,然后分为[1]和 [2,3,4,5]
一共执行了 n+ n-1 +n-2 +...1 = (1+n)*n/2 = 1/n + 1/n2 时间复杂度是 o(n2)
(来看最糟糕情况下的快排,当待排序的序列为正序或逆序排列时,且每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。)
最好情况:
假设每次第一个元素都是当前数组的中间值
那么第一次划分2个,第二次划分四个,第三次划分8个,
需要划分log2n次 (个数为n)
假设每次都遍历数组所有元素,所有的遍历次数是nlogn
*/
let arr = [3, 4, 5, 2, 1, 7, 2, 11]
function quicksort(arr, left, right) {
let pivot = arr[left]
let j = right
let i = left
// 退出条件
if (left >= right) return
while (i < j) {
while (arr[j] >= pivot && i < j) {
j--
}
while (arr[i] <= pivot && i < j) {
i++
}
// 现在找到了,要进行交换
if (i < j) {
let tmp = arr[j]
arr[j] = arr[i]
arr[i] = tmp
}
}
// 现在要把它和pivot交换
arr[left] = arr[i]
arr[i] = pivot
//交换完后在下一个数组分组里分治
quicksort(arr, left, i - 1)
quicksort(arr, i + 1, right)
}
quicksort(arr, 0, arr.length - 1)
console.log(arr);
========================================
最坏情况与最好情况:
最坏时间复杂度 o(n2)
当数组本身是一个有序数组时,如果以第一个元素作为pivot(枢纽、基准)
那么,每次分的时候,都是一边一个,另一边n-1个
需要遍历 n + n-1 + n-2 + n-3 +... + ... 1
即1+2+3+...n = (上底+下底)*高/2 = (1+n)n/2 = O(n2)
最好时间复杂度 o(nlogn)
最好的情况是每次都能均匀的划分序列
如果第一个元素作为pivot ,每次这个pivot恰好是数组的 中间值
那么会分成左右两边 设每层需要的时间最坏是n(也就是所有的遍历一遍),
下面看一下每次分层后,这个一共有多少层,
第一层是一个数组(2^0),第二层是2个数组(2^1),第三层是4个数组(2^2),第四层是8个数组(2^3)
... 到最后一层会有n个数组, 那么一共会有 (2^x = n ; x = logn)层
注: log2n 简记为 logn 因为https://www.cnblogs.com/eret9616/p/12929769.html
所以最坏总遍历次数是层数*循环的列为 logn*n 即为 nlogn
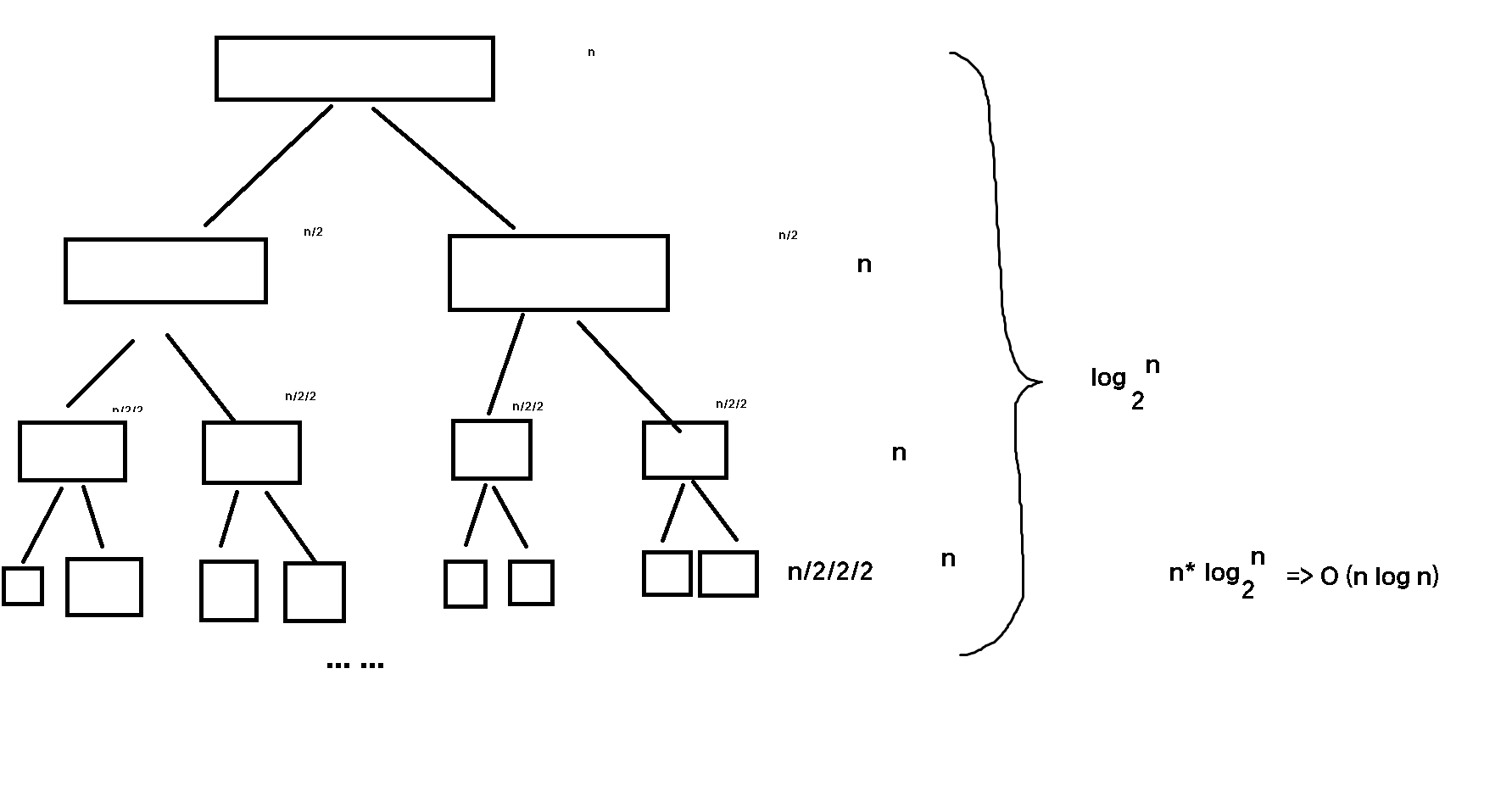
平均时间复杂度 O(nlogn)
这个需要一些数学工具,推理过程比较复杂,记住结论就行
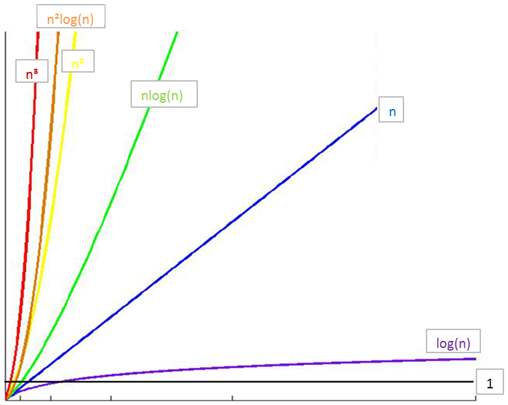
复杂度图像