Maxima可以画出Chaos、Duffing 、Fern、Lorenz、Rossler 、Portraits 、Mandelbrot、Staircase、Triangles等有趣的图...
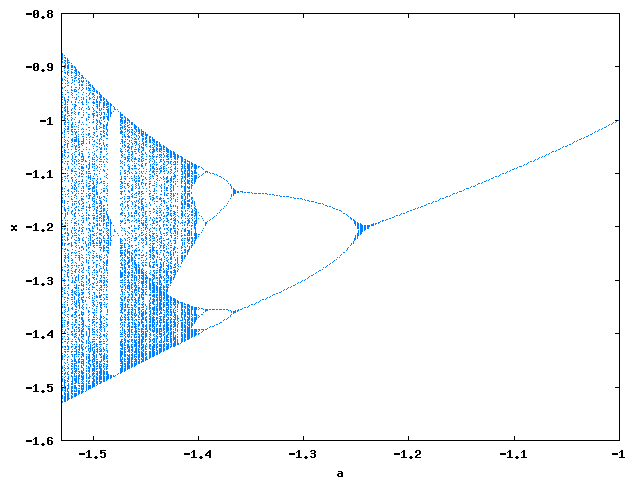
Chaos
orbits(x^2+a, 0, 100, 400, [a,-1,-1.53], [x,-1.6,-0.8],
[nticks, 400], [style,dots], WEB_IMAGE);
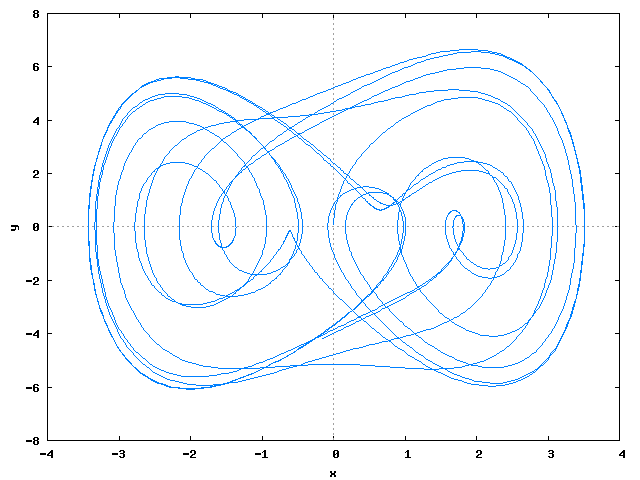
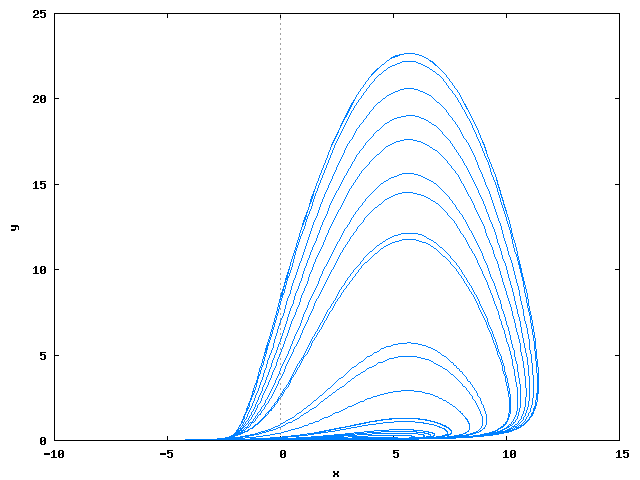
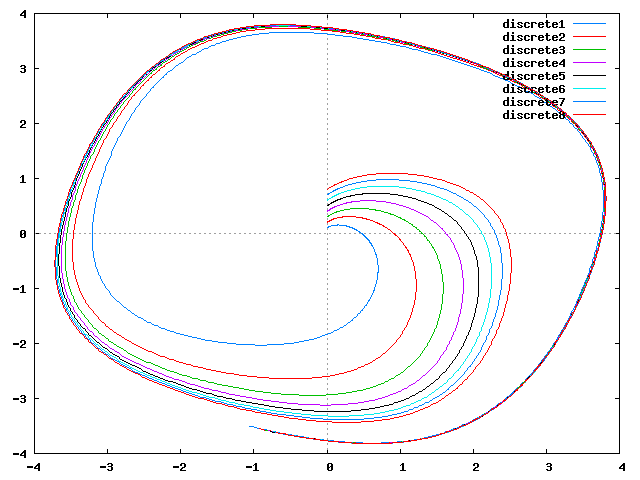
Duffing √
a:1.0;
b:0.3;
c:0;
f:10.0;
eqs:[y,-(a*x^3+c*x+b*y)+f*cos(t)];
t_range:[t, 0, 40, 0.01];
inits:[0.0, 0.1];
sol:rk(eqs,[x,y],inits, t_range)$
plot2d([discrete, makelist([sol[i][2], sol[i][3]], i, 1, length(sol))], WEB_IMAGE);
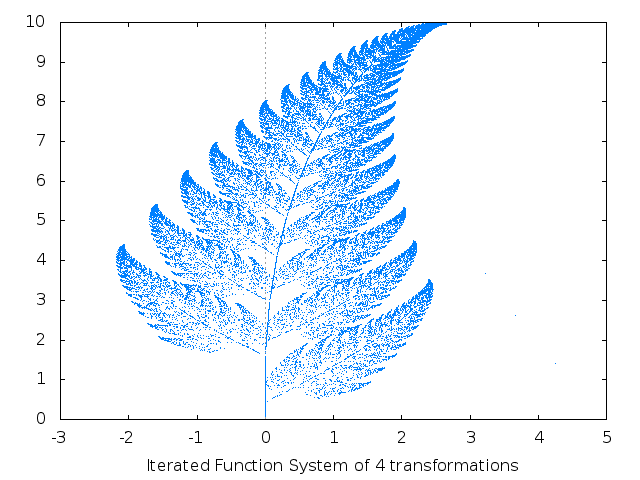
Fern
a1: matrix([0.85,0.04],[-0.04,0.85])$
a2: matrix([0.2,-0.26],[0.23,0.22])$
a3: matrix([-0.15,0.28],[0.26,0.24])$
a4: matrix([0,0],[0,0.16])$
p1: [0,1.6]$
p2: [0,1.6]$
p3: [0,0.44]$
p4: [0,0]$
w: [85,92,99,100]$
ifs(w, [a1,a2,a3,a4], [p1,p2,p3,p4], [5,0], 50000, [style,dots], WEB_IMAGE);
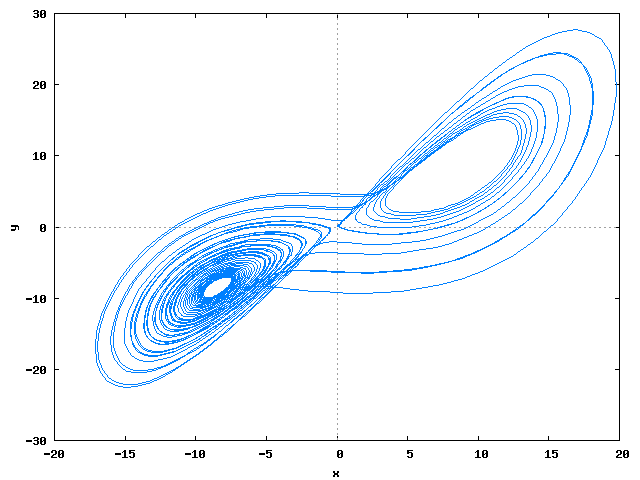
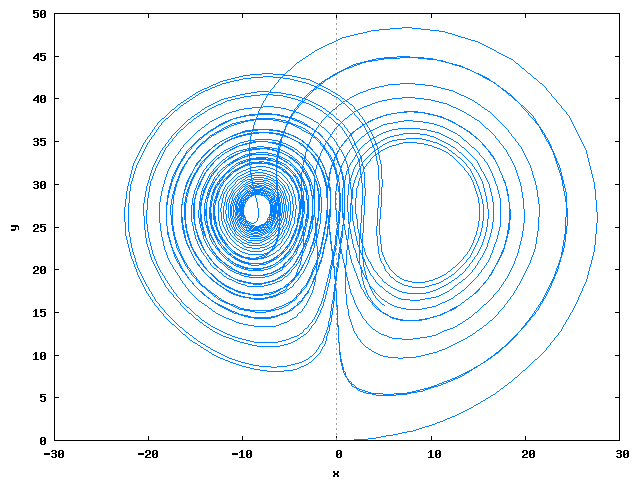
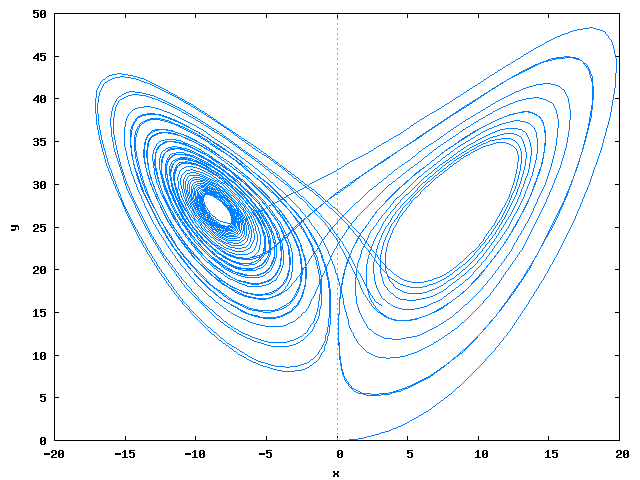
Lorenz √
d:10;
r:28;
b:8/3;
eqs:[d*(y-x),r*x-y-x*z, x*y-b*z];
t_range:[t, 0, 40, 0.01];
inits:[0.0, 0.1,0.0];
sol:rk(eqs,[x,y,z],inits, t_range)$
plot2d([discrete, makelist([sol[i][2], sol[i][3]], i, 1, length(sol))], WEB_IMAGE);
plot2d([discrete, makelist([sol[i][3], sol[i][4]], i, 1, length(sol))], WEB_IMAGE);
plot2d([discrete, makelist([sol[i][2], sol[i][4]], i, 1, length(sol))], WEB_IMAGE);
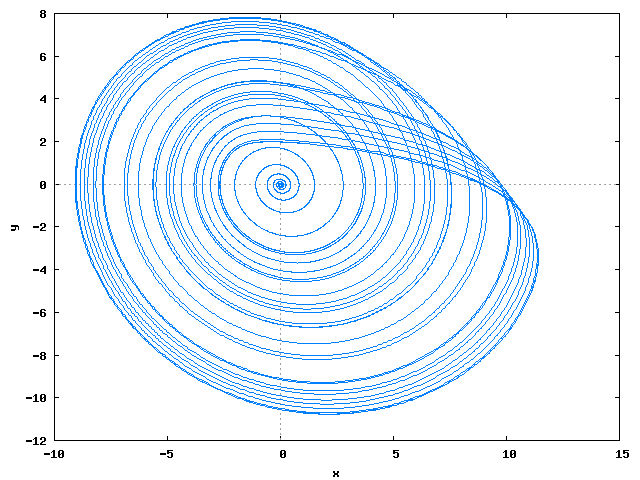
Rossler √
a:0.2;
b:0.2;
c:5.7;
eqs:[-y-z, x+a*y, b+x*z-c*z];
t_range:[t, 0, 200, 0.01];
inits:[0.0, 0.01, 0.01];
sol:rk(eqs,[x,y,z],inits, t_range)$
plot2d([discrete, makelist([sol[i][2], sol[i][3]], i, 1, length(sol))], WEB_IMAGE);
plot2d([discrete, makelist([sol[i][2], sol[i][4]], i, 1, length(sol))], WEB_IMAGE);
plot2d([discrete, makelist([sol[i][3], sol[i][4]], i, 1, length(sol))], WEB_IMAGE);
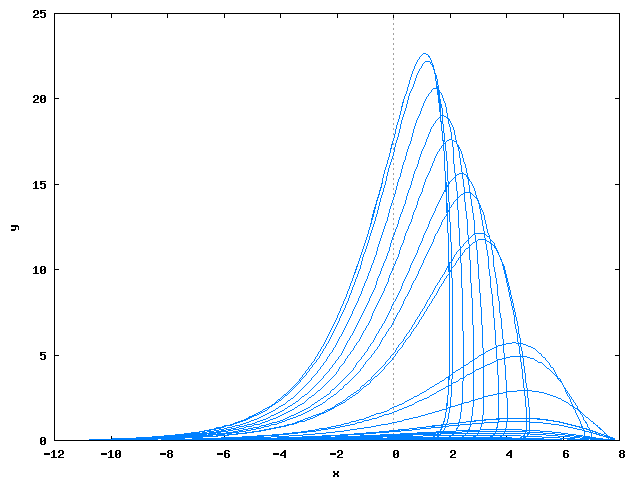
Portraits √
numPortraits:8;
eqs:[sin(x)+y, sin(y)-x];
t_range:[t, 0, 10, 0.01];
for k:1 thru numPortraits do (
inits:[0.0, k*0.1],
sol[k]:rk(eqs,[x,y],inits, t_range)
)$
sol_list:makelist(
[discrete, makelist([sol[k][i][2], sol[k][i][3]], i, 1, length(sol[k]))],
k, 1, numPortraits)$
plot2d(sol_list, WEB_IMAGE)$
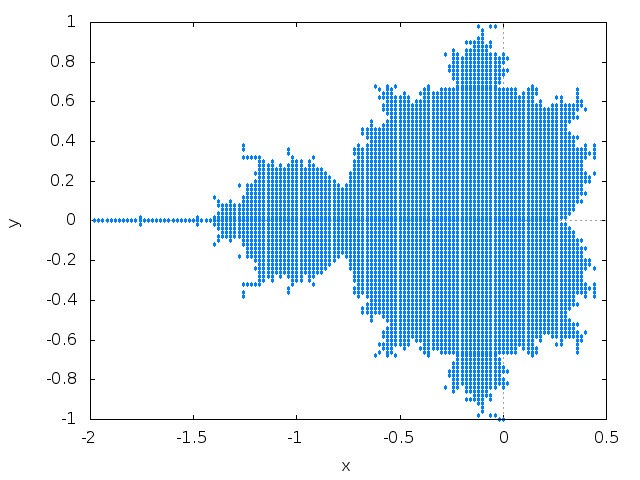
simple Mandelbrot
mandel(reMin, reMax, imMin, imMax, resolution, iterations):=block(
[reZ, imZ, absZ, i, pixels, reTemp],
pixels:[[0,0]],
for x:reMin step resolution thru reMax do [
for y:imMin step resolution thru imMax do [
reZ:0,
imZ:0,
absZ:0,
for i:1 step 1 thru iterations while absZ < 4 do [
reTemp:reZ^2 - imZ^2 + x,
imZ:2*reZ*imZ + y,
reZ:reTemp,
absZ:reZ^2+imZ^2
],
if absZ < 4 then pixels:append(pixels,[[x,y]])
]
],
return(pixels)
)$
plot2d([discrete, mandel(-2,0.5,-1,1, 0.02, 16)],[style,
[points,1,1,1]], WEB_IMAGE);
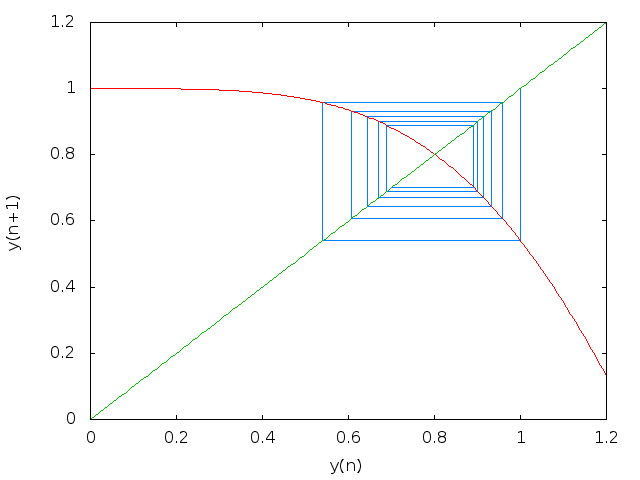
Staircase
load("dynamics")$
staircase(cos(y^2), 1, 11, [y, 0, 1.2], WEB_IMAGE);
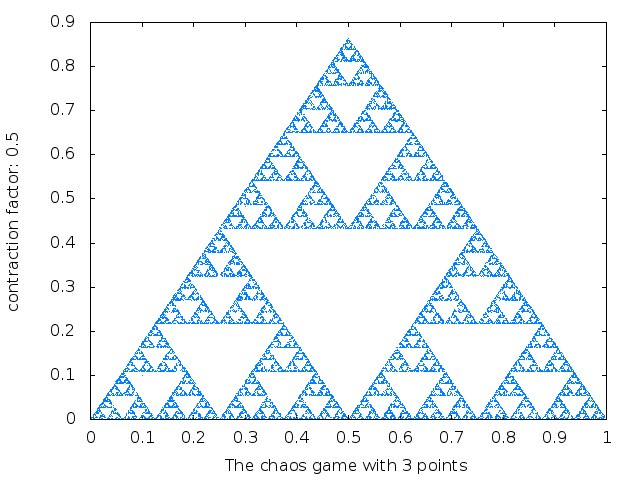
Triangles
chaosgame([[0, 0], [1, 0], [0.5, sqrt(3)/2]], [0.1, 0.1], 1/2,
30000, [style, dots], WEB_IMAGE);
Maple中可以试着画出:
Duffing
Lorenz
Rossler
Portraits