codeforces 786B Legacy

题目链接：codeforces 786B

线段树优化建边的模板题

注意到暴力建边是(O(qlen))，显然会超时

这种区间的问题一般把它放到线段树上有奇效，那我们就放到线段树上，线段树上的一个节点表示它所代表区间的连边情况

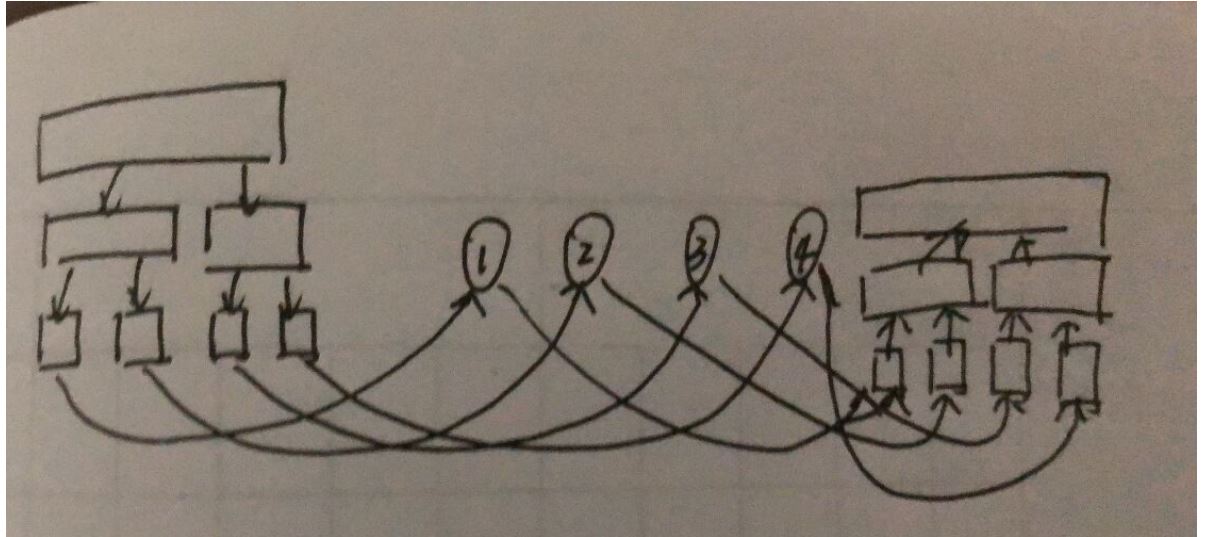
发现放在一棵线段树上效果好像也不明显，那就放在两棵线段树上

我们用一棵线段树来起到进入某个点的作用，另一棵起到走出某个点的作用

初始化时，第一棵线段树的父亲节点向儿子节点连边权为(0)的边，叶子结点向其代表的图上节点连边

具体的，对于一个节点([l,r])，将其连向([l,mid])和([mid+1,r])。特别的，当(l=r)时，线段树上的该点连向图上编号为(l)的点

另一棵线段树的操作类似，但是一条边的两端正好相反

大概就是这样的一个东西

接下来考虑询问

若(op=1)，则直接连边

若(op=2)，对于区间([l,r])将其放到第一棵线段树上，首先这个区间会被拆成(log)段，我们将(u)连向这些区间，权值为给定的(w)，根据线段树上的子孙关系，这个操作等价于连向了([l,r])中的所有点（经过若干条权值为(0)）的边

若(op=3)，我们将这个区间放到第二颗线段树上，它也会被拆成(log)段，让这些区间连向(u)，权值为(w)，则对于任意在([l,r])区间的点(v)，它首先可以走到第二棵线段树的对应叶子结点上，之后一直向上走一定能走到([l,r])拆出来的区间之一

于是我们的点数索然变成了(O(5n))，但是边数减少到了(O(qlogn+4n))，可以直接跑(dijkstra)求解最短路

#include<iostream>
#include<string.h>
#include<string>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define lowbit(x) (x)&(-x)
#define fir first
#define sec second
#define rep(i,a,b) for (register int i=a;i<=b;i++)
#define per(i,a,b) for (register int i=a;i>=b;i--)
#define maxd (ll)1e18+7
typedef long long ll;
const int N=1000000;
const double pi=acos(-1.0);
struct edgenode{
	int to,nxt,cost;
}sq[8002000];
int all=0,head[4001000];

struct hnode{
	int u;ll dis;
};
bool operator<(const hnode &p,const hnode &q)
{
	return p.dis>q.dis;
}
priority_queue<hnode> q;

int n,m,s,tot=0;
ll dis[4001000];
bool vis[4001000];

int read()
{
	int x=0,f=1;char ch=getchar();
	while ((ch<'0') || (ch>'9')) {if (ch=='-') f=-1;ch=getchar();}
	while ((ch>='0') && (ch<='9')) {x=x*10+(ch-'0');ch=getchar();}
	return x*f;
}

void add(int u,int v,int w)
{
	all++;sq[all].to=v;sq[all].nxt=head[u];sq[all].cost=w;head[u]=all;
}

void build1(int id,int l,int r)
{
	tot=max(id,tot);
	if (l==r)
	{
		add(id+n,l,0);
		return;
	}
	int mid=(l+r)>>1;
	build1(id<<1,l,mid);
	build1(id<<1|1,mid+1,r);
	add(id+n,(id<<1)+n,0);
	add(id+n,(id<<1|1)+n,0);
}

void build2(int id,int l,int r)
{
	if (l==r)
	{
		add(l,id+tot+n,0);
		return;
	}
	int mid=(l+r)>>1;
	build2(id<<1,l,mid);
	build2(id<<1|1,mid+1,r);
	add((id<<1|1)+n+tot,id+n+tot,0);
	add((id<<1)+n+tot,id+n+tot,0);
}

void modify1(int id,int l,int r,int u,int ql,int qr,int w)
{
	if ((l>=ql) && (r<=qr))
	{
		add(u,id+n,w);
		return;
	}
	int mid=(l+r)>>1;
	if (ql<=mid) modify1(id<<1,l,mid,u,ql,qr,w);
	if (qr>=mid+1) modify1(id<<1|1,mid+1,r,u,ql,qr,w);
}

void modify2(int id,int l,int r,int u,int ql,int qr,int w)
{
	if ((l>=ql) && (r<=qr))
	{
		add(id+n+tot,u,w);
		return;
	}
	int mid=(l+r)>>1;
	if (ql<=mid) modify2(id<<1,l,mid,u,ql,qr,w);
	if (qr>=mid+1) modify2(id<<1|1,mid+1,r,u,ql,qr,w);
}

void dij(int s)
{
	rep(i,1,N) dis[i]=maxd;
	dis[s]=0;q.push((hnode){s,0});
	while (!q.empty())
	{
		int u=q.top().u;q.pop();
		if (vis[u]) continue;vis[u]=1;
		int i;
		for (i=head[u];i;i=sq[i].nxt)
		{
			int v=sq[i].to;
			if (dis[v]>dis[u]+sq[i].cost)
			{
				dis[v]=dis[u]+sq[i].cost;
				if (!vis[v]) q.push((hnode){v,dis[v]});
			}
		}
	}
}

int main()
{
	n=read();m=read();s=read();
	build1(1,1,n);
	build2(1,1,n);
	while (m--)
	{
		int op=read();
		if (op==1)
		{
			int u=read(),v=read(),w=read();
			add(u,v,w);
		}
		else if (op==2)
		{
			int u=read(),l=read(),r=read(),w=read();
			modify1(1,1,n,u,l,r,w);
		}
		else if (op==3)
		{
			int u=read(),l=read(),r=read(),w=read();
			modify2(1,1,n,u,l,r,w);
		}
	}
	dij(s);
	rep(i,1,n) if (dis[i]!=maxd) printf("%lld ",dis[i]);
	else printf("-1 ");
	return 0;
}