在上个lecture中，我们看到了任意特定层是如何生成输出的，输入数据在全连接层或者卷积层，将输入乘以权重值，之后将结果放入激活函数（非线性单元）
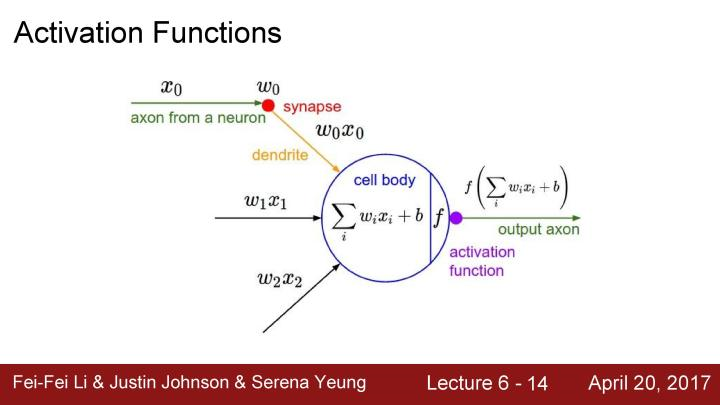
下面是一些激活函数的例子，有在之前使用过的sigmoid函数，之前提及到的ReLU函数。这里会提及更多的激活函数，并在它们之间进行权衡。
先是之前见过的sigmoid函数，每一个元素输入到sigmoid非线性函数中，并被压缩到0-1范围内。如果有一个非常大的输入值，那么输出结果将会非常接近1；如果有一个非常小的负值，那么输出结果将会非常接近于0。在横坐标接近于0的区域中，可以将这部分看成是线性区域，因为这有点线性函数。sigmoid函数曾经非常流行，因为它在某种意义上可以被看成是一种神经元的饱和“firing rate(放电率)"。当更为深入研究这个非线性函数，实际上它存在着几个问题。首先是饱和的神经元将会使得梯度消失。
下面是一个sigmoid gate，是计算图中的一个节点，将数据x作为输入，从sigmoid gate传出输出，这时让L对σ求偏导数，上游（upstream）梯度往回传播，然后乘以σ对x的偏导数，这是一个局部的sigmoid函数的梯度，把它们chain起来作为传递回来的下游梯度。当x=-10时会看到梯度的取值非常接近于0，因为这个值太过接近于sigmoid函数的负饱和区域，而这个区域几乎是平的，所以梯度也会接近于0。所以返回的上游梯度乘以一个约等于0的数值，会得到一个非常小的梯度，因此在某种意义上说经过链式法则的多次相乘后会使得梯度消失，这时零梯度便会传到下游的节点；同理当x=10时也是相同的情况。当x=0时会得到一个合理的梯度，并可以很好的进行反向传播。
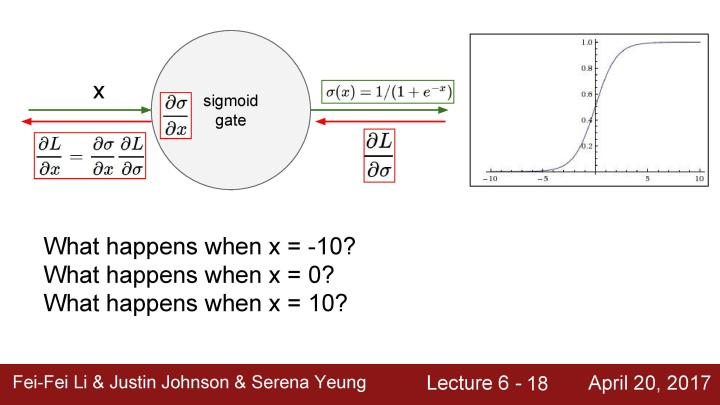
第二个问题是sigmoid是一个非零中心的函数。
当输入神经元的数值始终为正时，再乘以权值W，这时结果会要么全部是正数，要么全部是负数。这时把上游梯度传回来，就是损失L对f进行求导。
为正数或者负数，当任意传回来一些梯度乘以本地梯度（局部梯度），求关于权值w的梯度
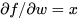，如果x的值总是正数，对w的梯度就等于
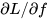乘以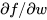
，此时就相当于把上游梯度的符号传回来，这意味着所有关于w的梯度全部为正值或全为负值，那么它们就会总朝着一个方向移动。当在做参数更新的时候，可以选择用同一个正数或者用不同的正数去增加所有w的值，或是用类似的方法减小w的值，这时会出现的问题是，这样更新梯度是非常低效的。看到下面右图的例子，假设w是二维的，所以可以用平面坐标轴来表示w，如果全为正或者全为负去进行更新迭代。我们得到两个象限，即在坐标轴上有两个区域，一个全为正（一象限）和一个全为负（三象限），这是根据梯度更新得到的两个方向，假设最好的w是图中蓝色向量，而实际的迭代过程如红色箭头所示，可以看到不能沿着w这个方向直接求梯度，因为这不是允许的两个梯度方向中的一个。所以在一般情况下要使用均值为0的数据，我们希望输入x的均值为0，就能得到正和负的数值，这就不会陷入上述梯度更新会出现的问题，因为这将会沿着同一方向移动。
**这里举一个简单例子，说明sigmoid函数的输出非零中心导致反向传播会w的梯度为全正或者全负是有问题的。假设我们有权值w=[1, -1, 1], 我们需要将权值更新为w =[-1, 1, -1], 如果梯度是同时有正和有负的，我们可以只更新一次就可得到结果：w=[1,-1,1]+[-2,2,-2] = [-1,1,-1]; 但是如果梯度只能是正或者只能是负，则需要两次更新才能得到结果； w = [1, -1, 1] + [-3, -3, -3]+[1,5,1]=[-1,1,-1]
第三个问题是这里使用了指数函数，这会消耗更多的计算能力，在网络的整体框架中，这个问题一般并不是主要的问题。因为进行卷积和点积的计算能力消耗会更大。
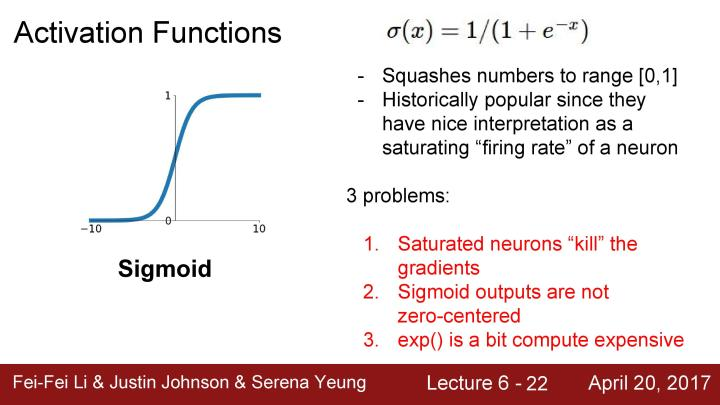
现在来看第二个要介绍的激活函数tanh, 它和sigmoid函数看起来非常相似，区别在于它现在被压缩在-1到1之间，同时它是以0为中心的，这就不会存在sigmoid函数的第二个问题；但从图像中看到它也存在几乎是平的区域，所以仍会存在梯度饱和的问题。
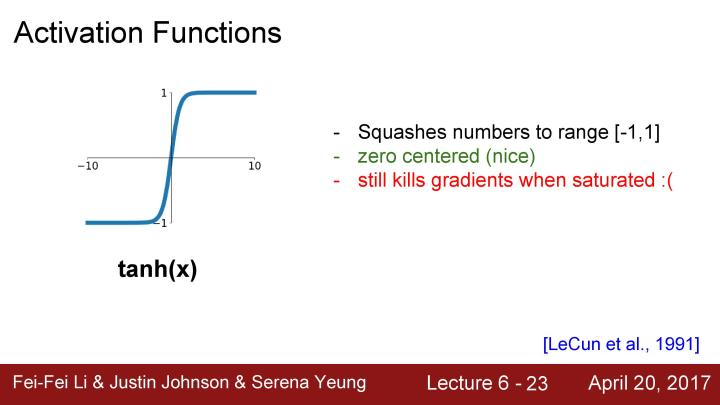
接下来看看ReLU这个激活函数，这个函数的形式为f(x) = max(0, x), 它在输入中按照元素进行操作，如果输入是负数，返回的结果是0，如果输入的是正数，返回结果是输入本身。这是经常使用的一个激活函数，它不会在正的区域产生饱和的现象，因为在一半的输入空间不会出现tanh和sigmoid中出现的梯度饱和问题，这是一个很大的优点。因为ReLU只是进行简单的max操作，所以在计算速度和收敛速度上都会比sigmoid和tanh快，同时也有研究证明ReLU比sigmoid更具备生物学上的合理性。然后对于ReLU，仍然存在一个问题，它不是以0为中心的函数，除此之外还有一个不好的地方是在负半轴会出现梯度不能更新的问题。
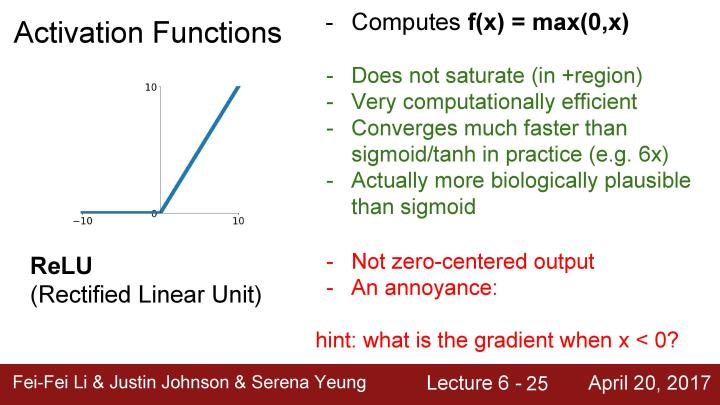
当x=-10时，对于ReLU函数此时梯度为0；而当x=10时，对于ReLU函数此时梯度不会为0；在线性区域内，当x=0时结果是不确定的，但在实践中，可以取x=0时的梯度为0，所以基本上在一半的区域内都会出现梯度消失的问题。
我们可以把这个问题称为dead ReLU，当在负半轴的区域中的时候，这里主要有几个可能的原因。如果观察数据云，假设这个就是全部的训练数据，可以看到这些ReLU可能处于的位置。这些RuLU基本上在平面中的一半区域能够产生激活，在这个平面区域内能够激活的又相应地定义了这些ReLU，可以看到这些dead ReLU基本不在数据云中，因此它从来不会被激活和更新，相比激活的ReLU，一些数据是正数，那么就能进行传递，一些则不会。主要有以下几个原因：第一是当有一个不好的初始化的时候，即权重设置非常的不好，它们恰巧不在数据云中，这就会出现dead ReLU的情况，这就导致不能得到一个激活神经元的数据输入，同时也不会有一个合适的梯度传回来，它不会被更新和激活。当学习率很大的时候，在这种情况下从一个ReLU函数开始，但因为在进行大量的更新，权重不断波动，然后ReLU单元会被数据的多样性所淘汰。这些会在训练时发生，它在开始阶段很正常，但在某个时间节点之后变差，最后挂掉。所以如果实际上你冻结了一个已经训练好的网络，然后将数据放进去，可以看到实际上网络中有10%到20%的部分是这些挂了的ReLU单元。大多数使用ReLU的网络都有这类问题，在实际运用中大家会深入检查ReLU单元。
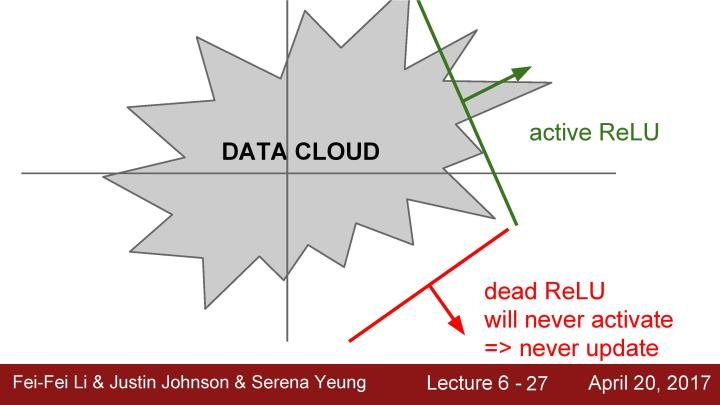
在实际应用时，大家也喜欢使用较小的正的偏置来初始化ReLU，以增加它在初始化时被激活的可能性，并获得一些更新，这基本上只是让更多ReLUs在一开始就处于能够被激活的状态，然而在实践中有些人认为这一点是有用的，也有的人认为没有，一般大家并不总是使用这个方法，大多数只是将偏置项初始化为0。
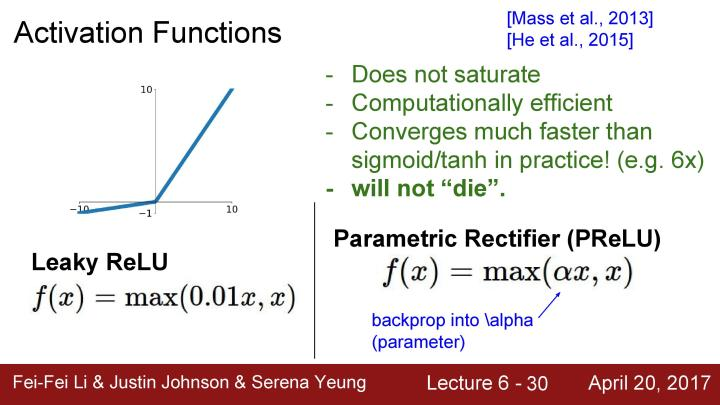
下面来看看基于ReLU的一些改进的激活函数，例如下面的Leaky ReLU, 这和原始的ReLU看起来很相似，唯一的区别是在负区间Leaky ReLU给出了一个微小的负斜率，这解决了之前ReLU中的dead ReLU问题，同时负区间中的计算仍然是非常高效的。
还有另外一个列子，简称PReLU，它与Leaky ReLU非常相似，在负区间也有这样的一个倾斜的区域，但是现在在负区间的斜率是通过α参数确定的。在这里不需要指定这个α，而是把阿尔法当作一个可以反向传播和学习的超参数，这就有了更多的灵活性。
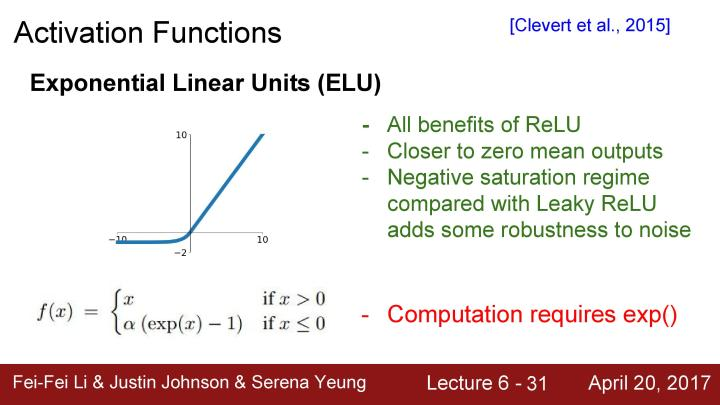
还有叫做Exponential Liner Unit，简称ELU的激活函数，它具有ReLU的所有优点，同时它的输出均值接近为0，但与Leaky ReLU相比较，ELU没有在负区间倾斜，在这里实际上在建立一个负饱和机制。这里有一些具有争议的观点认为，这样使得模型对噪声具有更强的robust，然后得到的这些更鲁棒(robust)的反激活状态。从某种意义上而言，这是一种介于ReLUs和Leaky ReLUs之间，同时具有Leaky ReLU所具有的曲线形状，使得输出均值更为接近于零。但是ELU也有一些比ReLU更饱和的行为。
下面这个叫做Maxout Neuron，它看起来有点不一样，因为它和其他的激活函数具有不相同的形式，并没有先做点积运算，而是把这个元素级别的非线性特征放在它的前面。相反，它是取两组w和x的点积加上b的最大值。所以它的作用是泛化ReLU和Leaky RuLU, 因为只是提取这两个线性函数的最大值。所以ELU给的是另一种线性机制的操作，这种方式不会饱和也不会挂掉，但问题在于会把每个神经元的参数数量翻倍，所以说如果每个神经元原有的权值集W,但是现在是原来的两倍。
所以在实际操作中，当考察所有这些激活函数的时候，一般最后的经验法则是使用RuLU，这是可用激活函数中最为标准的一种，并且在通常情况下，需要非常小心地调整学利率。但是也可以去尝试其他较为有难点的激活函数。