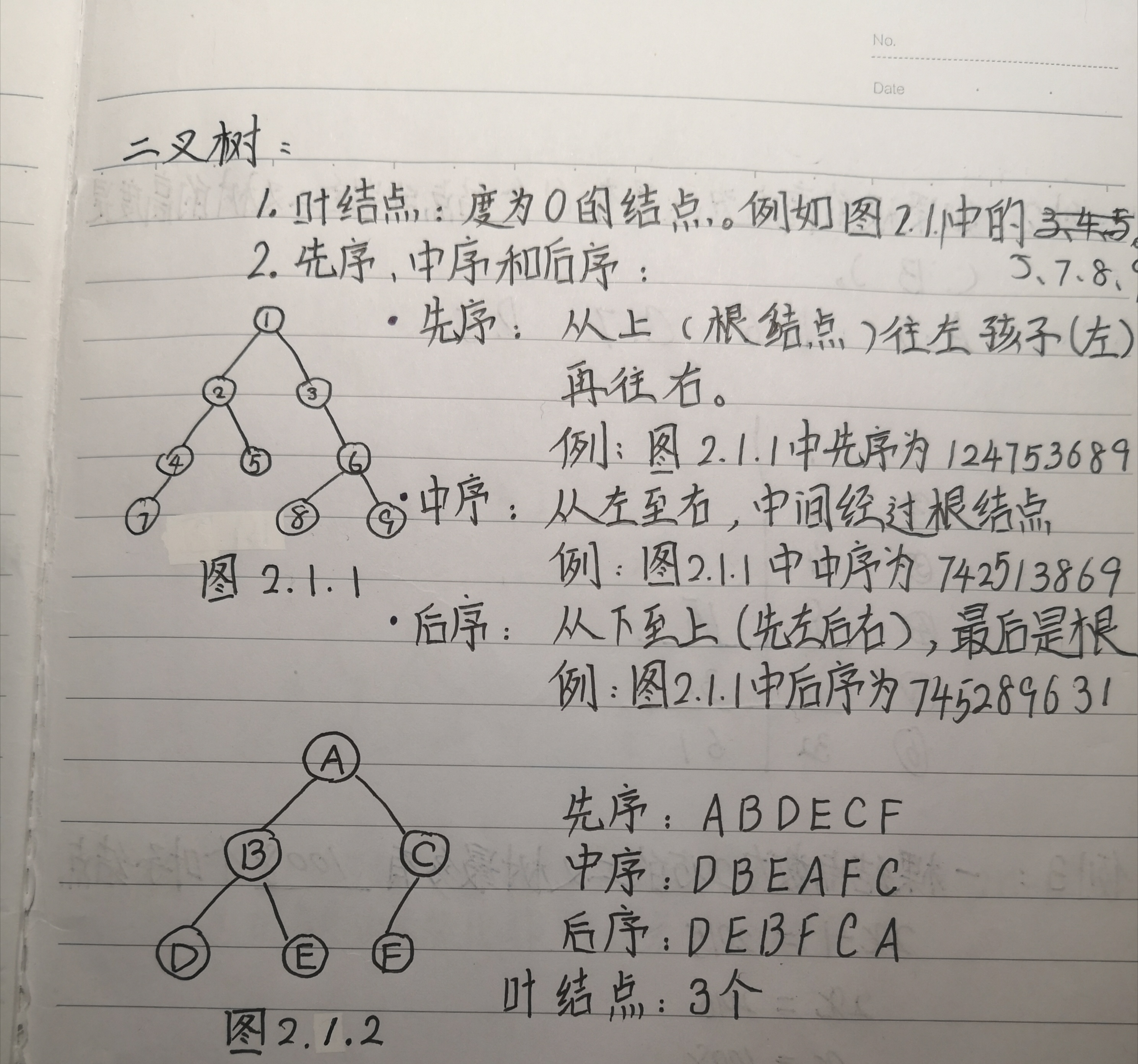
一、二叉树基本知识
二、二叉树先序遍历
题目:
输入一个整数n,表示二叉树中结点个数,编号为1~n。
1号结点为二叉树的根节点。然后输入n行,每行包括两个整数,第i行表示编号为i的结点的左、右子节点的编号。
如果某个结点没有左或右子节点,那么对应行的第一、二个整数为0。
输出此二叉树的先序遍历,每行输出一个编号。

#include<bits/stdc++.h> using namespace std; struct node{ int left; int right; }nodes[1000001]; void ds_pre(int u){ if(u == 0){ return; } cout << u << endl; ds_pre(nodes[u].left); ds_pre(nodes[u].right); } int main(){ int n; cin >> n; for(int i = 1;i <= n;i++){ int left,right; cin >> left >> right; nodes[i].left = left; nodes[i].right = right; } ds_pre(1); return 0; }
三、二叉树中序遍历
题目:
输入一个整数n,表示二叉树中结点个数,编号为1~n。
1号结点为二叉树的根节点。然后输入n行,每行包括两个整数,第i行表示编号为i的结点的左、右子节点的编号。
如果某个结点没有左或右子节点,那么对应行的第一、二个整数为0。
输出此二叉树的中序遍历,每行输出一个编号。
简化题目描述:刚才先序遍历时候的输出改为中序遍历的输出 : )

#include<bits/stdc++.h> using namespace std; struct node{ int left; int right; }nodes[100001]; void ds_md(int u){ if(u == 0){ return; } ds_md(nodes[u].left); cout << u << endl; ds_md(nodes[u].right); } int main(){ int n,root; cin >> n; for(int i = 1;i <= n;i++){ int left,right; cin >> left >> right; nodes[i].left = left; nodes[i].right = right; } ds_md(1); return 0; }
四、二叉树后序遍历
题目:
输入一个整数n,表示二叉树中结点个数,编号为1~n。
1号结点为二叉树的根节点。然后输入n行,每行包括两个整数,第i行表示编号为i的结点的左、右子节点的编号。
如果某个结点没有左或右子节点,那么对应行的第一、二个整数为0。
输出此二叉树的中序遍历,每行输出一个编号。
简化题目描述:刚才先序遍历时候的输出改为后序遍历的输出 : )

#include<bits/stdc++.h> using namespace std; bool vis[1000010]; struct node{ int left; int right; }nodes[10001]; void ds_bk(int u){ if(u == 0){ return; } ds_bk(nodes[u].left); ds_bk(nodes[u].right); cout << u << endl; } int main(){ int n; cin >> n; for(int i = 1;i <= n;i++){ int left,right; cin >> left >> right; nodes[i].left = left; nodes[i].right = right; } ds_bk(1); return 0; }
五、二叉树初赛例题


