前言
“各位,这可能是近期内最需要重视的sudo漏洞。”
程序员都知道,一句sudo可以“为所欲为”。

而现在,来自Qualys的安全研究人员发现,sudo中存在一个严重的漏洞:
任何本地用户,无需身份验证(密码),也能获得root权限。
也就是说,攻击者完全可以利用这个漏洞,直接接管主机系统!
什么样的漏洞
Qualys的研究人员指出,此漏洞是基于堆的缓冲区溢出。
利用这一漏洞,攻击者无需知道用户密码,一样可以获得root权限。并且,是在默认配置下。
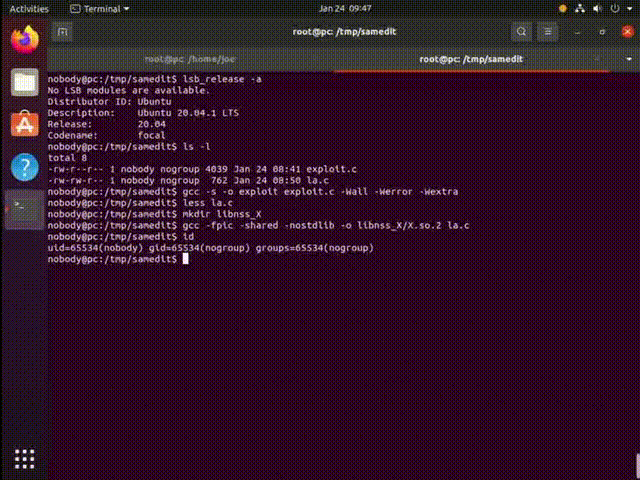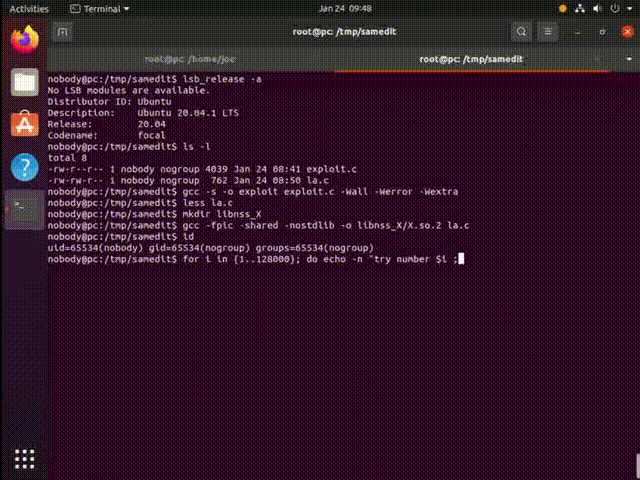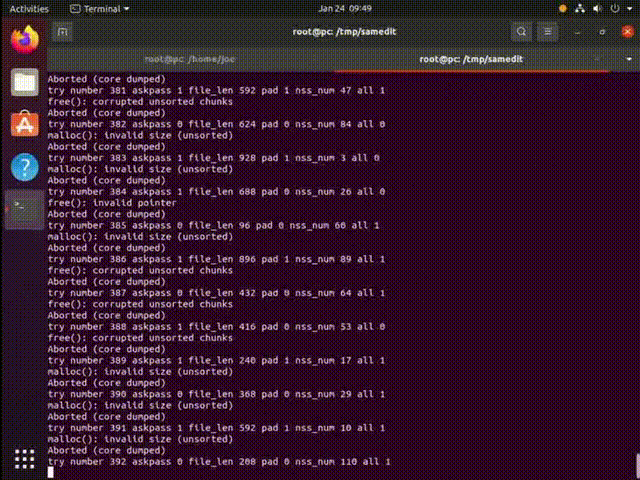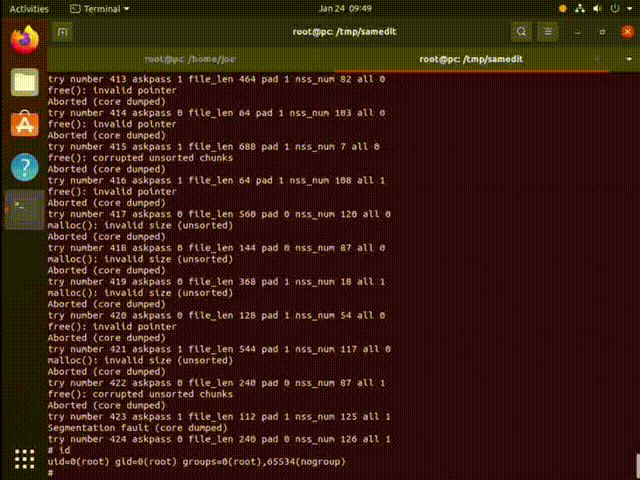
攻击效果
这一漏洞名为CVE-2021-3156(又名Baron Samedit)。Qualys分析认为,漏洞发生的原因在于sudo错误地转义了参数中的反斜杠。
通常,通过shell(sudo -s或sudo -i)运行命令行时,sudo会转义特殊字符。
但 -s 或 -i 也可能被用来运行sudoedit,在这种情况下,实际上特殊字符没有被转义,这就可能导致缓冲区溢出。
利用该漏洞,研究人员在多个Linux发行版上成功获得了完整的root权限,包括Ubuntu 20.04(sudo 1.8.31)、Debian 10(sudo 1.8.27)和Fedora 33(sudo 1.9.2)。
并且,Qualys认为,在这种情况下,sudo支持的其他操作系统和Linux发行版也很容易受到攻击,并不能排除风险。
漏洞10年前就存在
能让攻击者跳过身份验证,直接获取root权限,这个漏洞本身的严重程度,按理说应该引起大部分用户和开发者注意。
事实上,这个漏洞2011年7月开始就已经存在,是由8255ed69这个commit引入的。
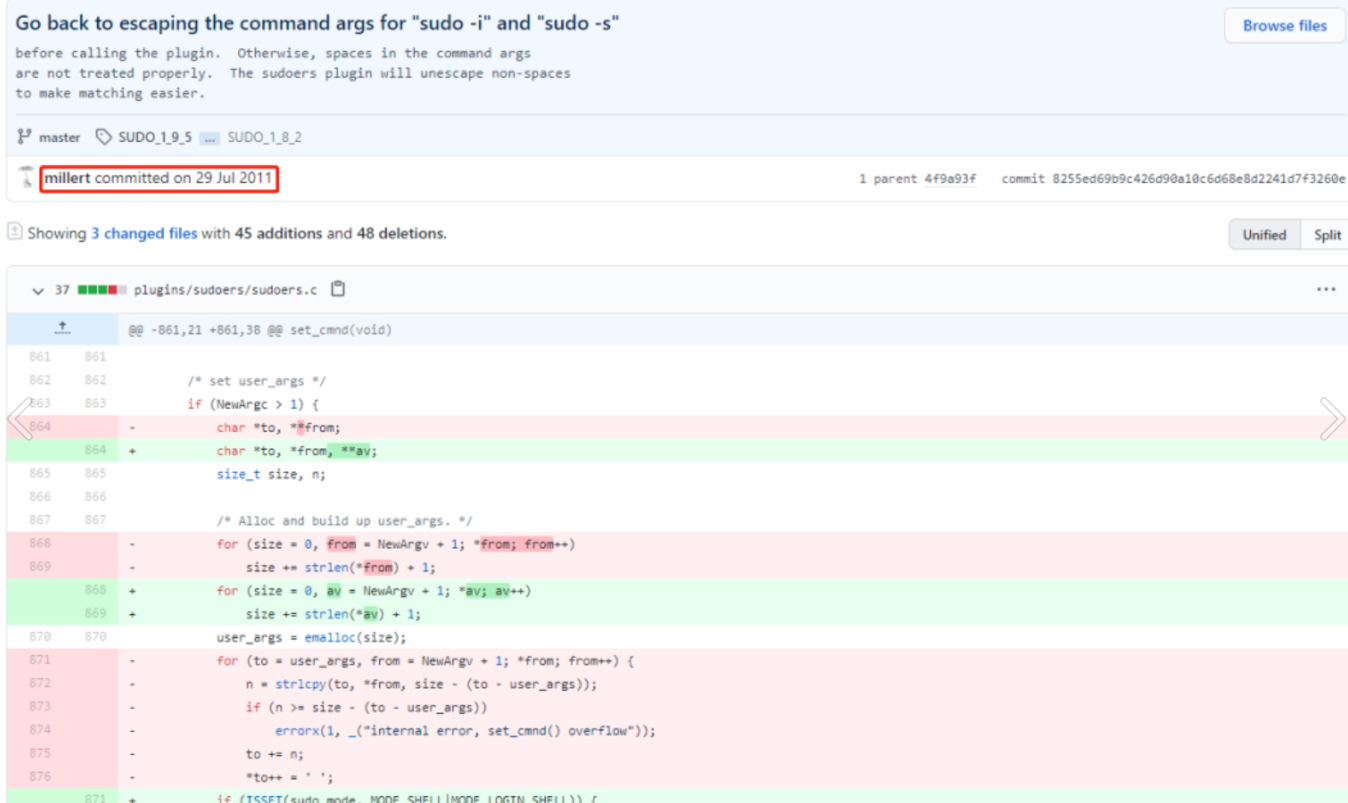
匪夷所思的是,从2011年7月29日提交到现在,一直没有人发现、修复由此引发的漏洞。
也就是说,这个漏洞一直存在于sudo1.9.0到1.9.5p1的所有稳定版本,和1.8.2到1.8.31p2的所有旧版本的默认配置中。
按照惯例,在Qualys公布这一漏洞的详细消息之前,sudo已经正式修复这个漏洞。
所以,升级到sudo的1.9.5p2或是更高版本,就能化解风险。
如何测试你现在使用的sudo版本是否存在漏洞呢?
首先你需要以非root用户的身份登录,并运行“sudoedit -s /”命令。
有漏洞的系统会抛出一个以 “sudoedit: ”开头的错误,而打过补丁的系统则会显示一个以 “usage:”开头的错误。
为啥10年未修复?
为什么提交近10年间,这个漏洞都没人理会呢?
在Hacker News上,有网友给出了推断:

他认为,包括但不限于sudo这样的Linux程序的用户提交声明,是从来没有经过测试的。
提交没有测试的bug声明,原作者是没有充足的理由相信bug的真实性,也就无所谓bug是否修复了。
比如去年,有苹果的安全人员也发现了一个类似的安全漏洞,Linux Mint上的sudo在非默认配置下,也允许用户跳过身份验证获得root权限。
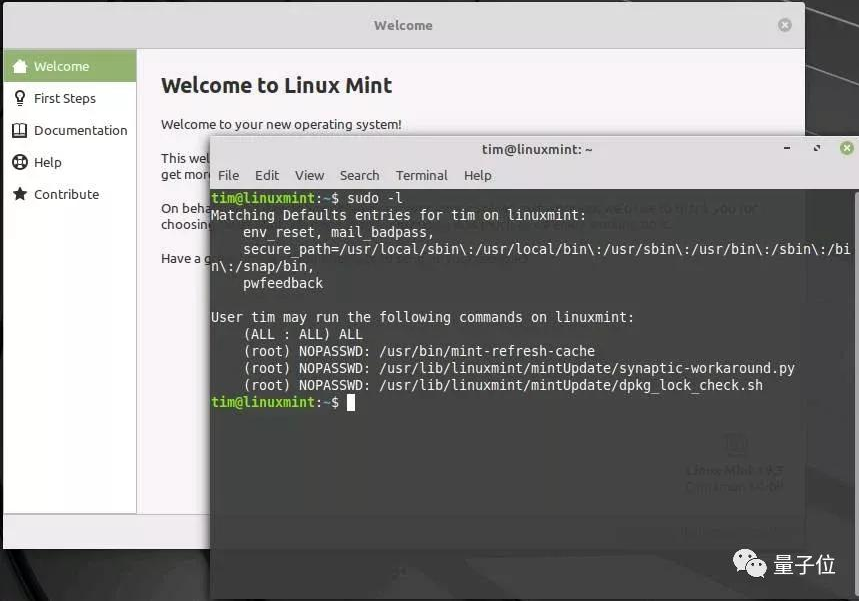
而类似这样的漏洞补丁,大部分也没有经过测试,所以,对用户来说,即使安装漏洞修复,也还存在漏洞修补不完全,以及引起新漏洞的风险。
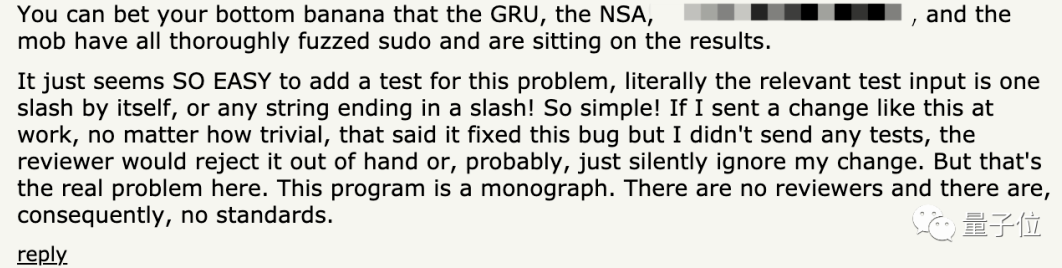
还有人说,sudo官方没有“审稿人”的职能,对于用户的提交,没有确定的安全标准,所以也不会有的测试和审核。
总结
普通用户怎么办呢?
很遗憾,现在根本没有一套完美的解决办法。
面对可能存在的漏洞,你能做的,就是格外留意自己的系统安全,避免不信任的用户碰到你的电脑。
总之入侵几漏洞分析是一个经验工作,只有不断提升攻防技术和分析各种攻防实际案例,你才能更好的做好服务器入侵检测以及服务器安全防御,因此这既是一个枯燥的工作,还需要你长期不断学习,很多时候技术经验是非常有用的。
参考链接:https://www.toutiao.com/i6922290280045576711/?tt_from=mobile_qq&utm_campaign=client_share×tamp=1612074171&app=news_article&utm_source=mobile_qq&utm_medium=toutiao_android&use_new_style=1&req_id=20210131142251010014047043211A93BD&share_token=735adfc7-18f2-4b01-b4eb-d5eaf7607fd3&group_id=6922290280045576711