4、加载栅格文件
栅格数据是GIS中重要的数据源之一,如卫星图像、扫描的地图、照片等。
栅格数据常见的格式有Bmp、Tiff、Jpg、Grid等。
添加栅格数据主要使用Rasterlayer 组件类,以及IMap、ILayer、IRasterLayer接口等。Rasterlayer组件类实现了ILayer、IRasterlayer、TTable、IDataset等接口,主要用于栅格数据的打开、显示、操作状态等设置。
介绍一种打开栅格文件的方法
核心代码:
#region 添加TIN数据 private void 添加TIN数据toolStripLabel1_Click(object sender, EventArgs e) { //方法: AddTinFile(); } /// <summary> /// 加载栅格图层 /// </summary> private void AddTinFile() { this.Cursor = Cursors.WaitCursor; IWorkspaceFactory pWorkspaceFactory = new TinWorkspaceFactoryClass(); IWorkspace pWorkspace = pWorkspaceFactory.OpenFromFile(m_Path, 0); ITinWorkspace pTinWorkspace = pWorkspace as ITinWorkspace; //声明一个pTin变量, 存储所打开的"tin" ITin pTin = pTinWorkspace.OpenTin("tin"); //将TIN变为TIN图层 ITinLayer pTinLayer = new TinLayerClass(); pTinLayer.Dataset = pTin; pTinLayer.Name = "TIN"; //也可以用三维空间AxSceneControl加载 //axSceneControl1.Scene.AddLayer(pTinLayer, true); this.axMapControl1.AddLayer(pTinLayer); this.Cursor = Cursors.Default; } #endregion
加载Tin文件到SceneControll对象和到MapControl对象的方法大同小异。
只需要将
this.axMapControl1.AddLayer(pTinLayer);
换成
axSceneControl1.Scene.AddLayer(pTinLayer, true);
补充说明:
需从工具箱中拖曳SceneControl到界面窗口,自动生成SceneControll对象。
Tin文件的加载需要用到两个组件类:Scene和SceneGraph。
Scene是一个矢量、栅格和图形数据显示与处理的容器,该类实现了IScene接口,提供了控制 Scene的方法和属性,如Addlayer方法用于向场景中增加一个图层。
SceneGraph是一个记录在Scene中出现的数据和事件的容器,该类实现了ISceneGraph接口,提供了控制和处理Scene中图形的方法和属性。
效果图:
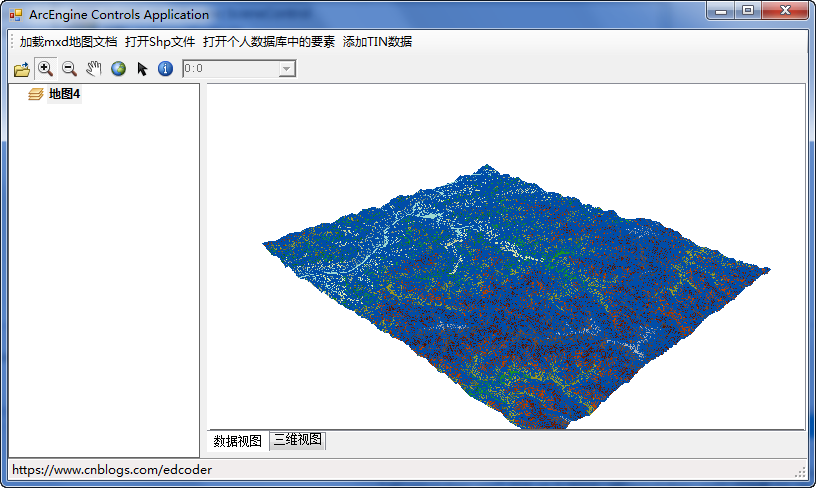
谢谢观看!本人初学GIS二次开发,如果有不对的地方,请多多包涵!