
壹 ❀ 引
十天前做的一道题了,一直没整理,今天才花时间去读了官方题解思路,这道题也凸显出了算法思路的重要性,执行耗时差的真不是一点半点。题目来自448. 找到所有数组中消失的数字,题目描述如下:
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
示例:
输入: [4,3,2,7,8,2,3,1] 输出: [5,6]
我们简单分析题目,看看有哪些方式可以做到。官方思路理解起来开始有那么点绕,没关系,我还是会画图把解题思路说清楚,那么本文开始。
贰 ❀ 憨憨做法,循环嵌套n²
我们来提取题目信息,一个包含n个数字的数组,每个数字的范围为1 ≤ a[i] ≤ n,也就是说,假设n为5,那么数组元素一定有5个,每个数字可取范围是[1,5],再加上某些元素会出现2次,所以必定会导致某些元素没有空间去存放它,从而导致缺失(有点抽屉原理的意思),而我们的目的就是要找到缺失的元素。比如:
[1,2,2,3,5]//缺了4
[1,1,2,2,3]//缺了4,5
以上面例子来说,因为我们已经知道a[i]范围为[1,n],所以只要知道知道1-n之间每个数有没有在数组中出现即可了,上代码:
/**
* @param {number[]} nums
* @return {number[]}
*/
var findDisappearedNumbers = function(nums) {
let len = nums.length,
ans = [];
// 注意这里是从1开始,因为范围是[1,n]
for(let i =1;i<=len;i++){
//判断nums里面有没有包含i,没有就加入ans
if(!nums.includes(i)){
ans.push(i);
};
};
return ans;
};
当然将上文中的includes替换成indexof来查找也是可以的。那么这种做法效率怎么样呢?当然不咋地,我们在外层需要遍历n次,而每次都得去数组里面查找一次谁没有,非常典型的O(n²)时间负责度。随着n范围越大,所需耗时会剧增。
叁 ❀ 使用哈希表,复杂度降为2n
有没有其它更好的做法呢,当然有,比如使用哈希表。我们可以将数组中每个出现的元素记录在哈希表中,设置为true,表示它出现过,这样遍历一次我们就得到了一份记录了所有出现过数字的哈希表了。
之后拿这个哈希表去和[1,n]对比,只要不为true的很明显是没出现的,那就是我们想要找到的缺失元素了,直接上代码:
/**
* @param {number[]} nums
* @return {number[]}
*/
var findDisappearedNumbers = function(nums) {
let len = nums.length,
hash = {},
ans = [];
if (!len) {
return ans;
};
// 在哈希表中记录出现过的数字
nums.forEach(num => hash[num] = true);
for (let i = 1; i <= len; ++i) {
// 没有就是undefined
if (!hash[i]) {
ans.push(i)
};
};
return ans;
};
有同学就要问了,这思路不是跟上面差不多吗,思路是差不多,但是从此时时间上已经降为2n了,按照规律省去系数2,时间复杂度其实是O(n)。同学们,这个时间提升那就是质的飞跃了,我们可以假象n为1000,即便是2n也才2000,但上面的做法就是10000000了。
肆 ❀ 原地修改数组
还有没有其它做法呢,当然有,通过原地修改数组的做法,理解起来可能有点绕,我尽量说清楚点。
在上文中我们已知,这个数组有几个元素比如5个,那么数组中最大的数不会超过5。而我们知道数组长度为5,最后一个数的索引其实是4。也就说,我们可以找到任意一个数,减去1,都能对应到数组中某个元素。
可能大家还没get到这个点,拿个例子来说,比如现在有数组[1,2,3,3,3];
我们从索引0开始遍历,拿到第一个元素,1,减去一个1。为什么要减去1?因为以a[i]此时的范围是[1,5],减去1不正好对应了数组索引0-4吗?好了,此时a[0]其实就是自己,我们将它变成负数,也就是-1。此时数组为[-1,2,3,3,3]。
继续第二次遍历,第二个数字是2,减去1,a[1]正好是2,于是我们也将其变成负数,此时数组为[-1,-2,3,3,3]。
紧接着第三次遍历,我们拿到3,减去1,将其索引的数变负数,此时数组就是[-1,-2,-3,3,3]。
继续第四次遍历,我们又拿到3,减去1,a[2]此时已经是负数了,不做操作。
最后一次遍历,我们还是拿到3,由于是负数,一样不作操作。
于是我们拿到最终数组[-1,-2,-3,3,3]。而通过前面知道,凡是负数的说明其索引加1的数都是存在的。而正数的这两个的索引加1,正好是我们所缺的[4,5],这不就是我们想要的答案吗。
让我们上代码:
/**
* @param {number[]} nums
* @return {number[]}
*/
var findDisappearedNumbers = function(nums) {
let len = nums.length,
ans = [];
if (!len) {
return ans;
};
// 1-n开始,有n个,那么n-1一定能对应到一个索引
for (let i = 0; i < len; i++) {
let num = Math.abs(nums[i]);
// 注意,如只有是正数的情况我们才转负数
if (nums[num - 1] > 0) {
nums[num - 1] *= -1;
}
};
for (let i = 0; i < len; i++) {
// 正数的索引加1,就是我们缺失的数了
if (nums[i] > 0) {
ans.push(i + 1);
};
};
return ans;
};
最后,上一张三种方案时间耗时对比图。
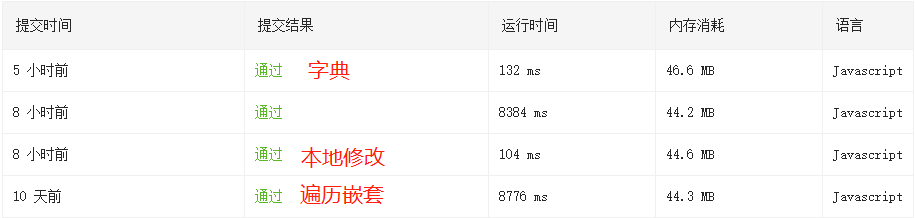
你看,让数组遍历降维,真的是巨大的优化啊。