在做阿里的o2o优惠券预测的时候学习了GBDT。听闻GBDT的威力,自然要学习学习。
接下来从以下几个方面记录下我对于GBDT的理解。
GBDT的用途,优势
GBDT的结构和算法流程
GBDT如何训练
Sklearn 的GBDT使用,参数意义
GBDT的用途,优势:
GBDT(Gradient Boosting Decision Tree) 又叫 MART(Multiple Additive Regression Tree),是一种迭代的决策树算法,
该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。
GBDT可以用于分类,也可以用于回归,并且还可以用户特征的筛选。
GBDT的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合。业界中,Facebook使用其来自动发现有效的特征、特征组合,来作为LR模型中的特征,以提高 CTR预估(Click-Through Rate Prediction)的准确性
GBDT的概念:
GBDT 的全称是 Gradient Boosting Decision Tree,梯度提升决策树。Boosting方法是使用一组弱学习器提升为一个强学习器的方法。要求这些弱学习器是各不相同的,也就是对于同一样本要求有不同的预测结果(如果相同就没有组合的必要了,毕竟是要长短互补的)。还要求这些学习器的准确率要比随机猜好一些。
DT也就是Decision Tree,决策树。决策树分为回归树和分类树两大类。GBDT使用的是分类树。
GBDT的结构和算法流程:
GBDT,
GBDT由多棵树组成,每棵树是回归树。
GBDT的多棵树组合方式与Adaboost的方式不一样。GBDT的每棵树都是学习上一棵树的残差,也就是在上一棵树学习的结果上继续学习。
这样做的好处就是如果上一棵树完全正确分类,在下一颗树上就不需要学习了,对于误差比较大的才需要继续学习。
举个例子,参考自一篇博客(参考文献 4),该博客举出的例子较直观地展现出多棵决策树线性求和过程以及残差的意义。
训练一个提升树模型来预测年龄:
训练集是4个人,A,B,C,D年龄分别是14,16,24,26。样本中有购物金额、上网时长、经常到百度知道提问等特征。提升树的过程如下:
训练一个提升树模型来预测年龄:
训练集是4个人,A,B,C,D年龄分别是14,16,24,26。样本中有购物金额、上网时长、经常到百度知道提问等特征。提升树的过程如下:
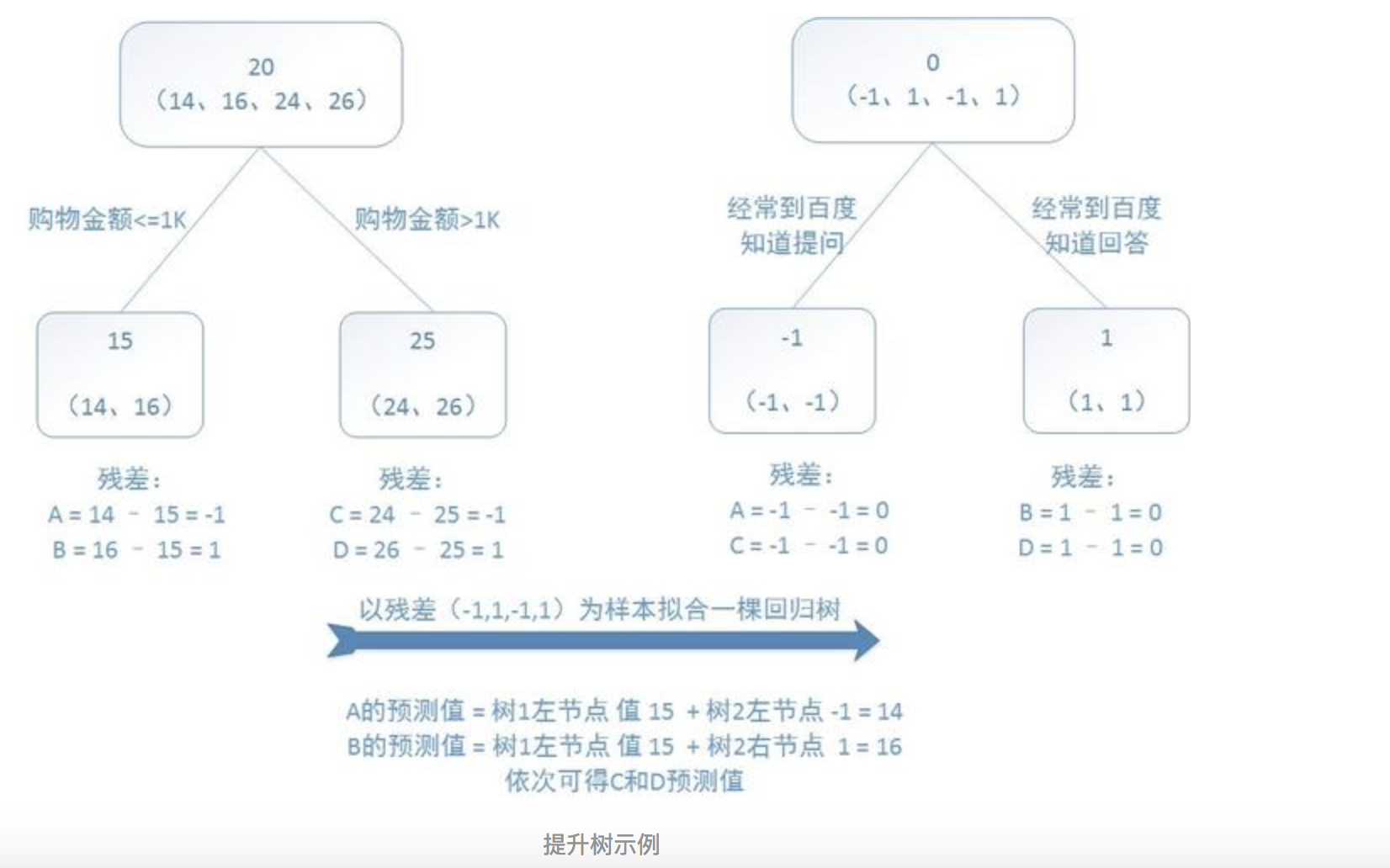
图中是直接选取了平均值作为预测值,然后通过真实值减去预测值计算残差 。第二棵树学习上一棵树的残差。
在实际使用过程中GBDT算法还有一些问题,即如何划分树,如何确定预测的函数,如何计算残差,如何训练。
(1)如何划分树,也就是我们使用哪一个属性的哪一个值来作为划分条件进行划分。
对于每个特征,尝试这个特征的可能的值进行划分,(如果是连续值的话,可以参考西瓜书,对于连续值的处理)
选择的标准是最小化平方误差,但是也不都是这一个代价函数。
选择第J个变量xi 和他的取值S,作为切分变量和切分点。并且定义两个区域:

然后寻找最优的切分变量J和最优切分点S。具体的,求解:
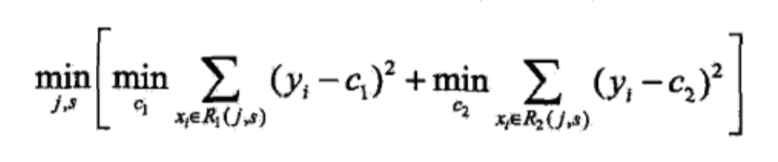
(2)如何确定训练的函数
每一棵树都是一个回归树,用一个线性函数去拟合目标值,不一定是用平均值。
每迭代一轮就是多一个树,来对上次的残差进行训练。
(3)如何计算残差
使用梯度的绝对值拟合残差,还要乘以一个学习率
(4)如何训练
每轮迭代的时候,首先要使用上一轮训练完的残差来训练出本轮的决策树
要训练出来的这个决策树,加上之后,使得整体的代价函数的值最小。
关于GBDT的损失函数,正则化部分看明白了再继续写
参考资料:
shttps://www.jianshu.com/p/005a4e6ac775
《统计学习原理》