线性回归 机器学习实战笔记

前言：

刚开始看到线性回归，总觉得这是不是和罗辑回归又啥关系。

对比一下吧。

线性回归用于数值预测，罗辑回归用于分类。

对于罗辑回归 来说，用于分类的神经网络的最后一层也是一个罗辑回归。

线性回归：

线性回归比较简单，找到一条最佳直线来拟合数据。拟合的目标可以是均方误差最小。

求最优的线性回归直线的解法就是使用最小二乘法，通过最小二乘法来解。

但是这种做法存在问题。存在的问题主要有 非线性的数据无法拟合，容易欠拟合。

使用最小二乘法，求解的时候有矩阵推导这部分还不会啊

 对于Y = XW，矩阵表示均方误差是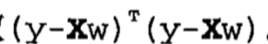 

然后对w求导，然后得到

（这部分对于矩阵求导没有看明白啊，也是艰难）。

然后另导数等于零求的极小值。

改进的方法有以下几种：

（1）局部加权线性回归

（2）岭回归

（3）前向逐步线性回归

首先说说局部加权线性回归。这个的主要思想是当前待预测点越近的点，对于拟合的影响越大。这个影响是使用核函数来实现的。

核函数一般选用高斯核，例如：

 其中对于预测结果影响比较大的是K。其中K可以理解为对于待预测点来说，参与线性拟合的点的范围，K值越大参与线性拟合的范围越大，如果K=1，则基本就是直线了。这部分为何会这样还没想明白。

一下内容是我主要的参考资料了。其中的D就是权重了。

LWLR

即 Locally Weighted Linear Regression(局部加权线性回归)。 
其优化目标函数是 

 

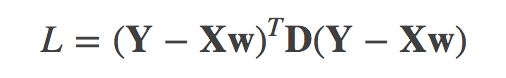
其中 D是N×N的对称矩阵，其元素值d(i,j)表示数据xi与xj的某种关系的度量。

对L关于w求导，得 

令导数为0解得w: 

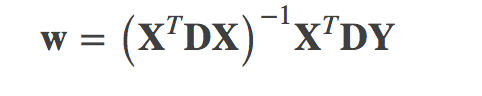
d(i,j)的函数称为“核”，核的类型可以自由选择，最常用的是高斯核： 

d(i,j)=exp(||xi−xj||1−2k2)

观察上式可得：d(i,j)与xi、xj的L1范数呈负相关，L1范数越大，值越小；与|k|呈正相关。

当|k|取一个很小的值时，d(i,j)的值随||xi−xj||1的增加衰减速度极快，这时矩阵D非对角线上的元素都为0，对角线上元素值都为1，退化为普通的LR。由此可知，LWLR是LR的推广形式。

 参考资料：

《机器学习实战》

http://blog.csdn.net/golden1314521/article/details/46778039