The 2014 ACM-ICPC Asia Xi'an Regional Contest — F题 Color

觉得这题真要总结一下，先贴一个半AC的代码（还有组合数超时问题）。

1）西安赛场上我们推出了一个dp方程：

定义前i个位置使用了j种颜色的花(一共备选m种)：

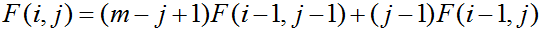
边界是F(1,1) = m，答案是F(n, k)。很显然直接递推的方式是O(nk)的复杂度，显然受不了。然后我们很sb的在赛场上搞各种矩阵快速幂压缩方法，10⁶的矩阵，最后这个dp方程成功铸铁。

2）不这样想应该怎么思考呢？如果我们换一个角度，让N个位置固定，

凭直觉我们能想出C(m, k) * k * (k-1)^n-1这么一个式子，对不对呢？显然它是能保证相邻两朵花不同颜色了，但并不能保证刚好用k朵花(例如有花1、2、3，K=3，N=3，那么121也被计算在内了）。

难道做不通了么？。。。如果将F[i, j]定义为在i朵备选花中，选j朵的方案数：

这是一个方法，因为它的复杂度终于跟M和N无关了，我们对它进行化简和二项式反演：

 

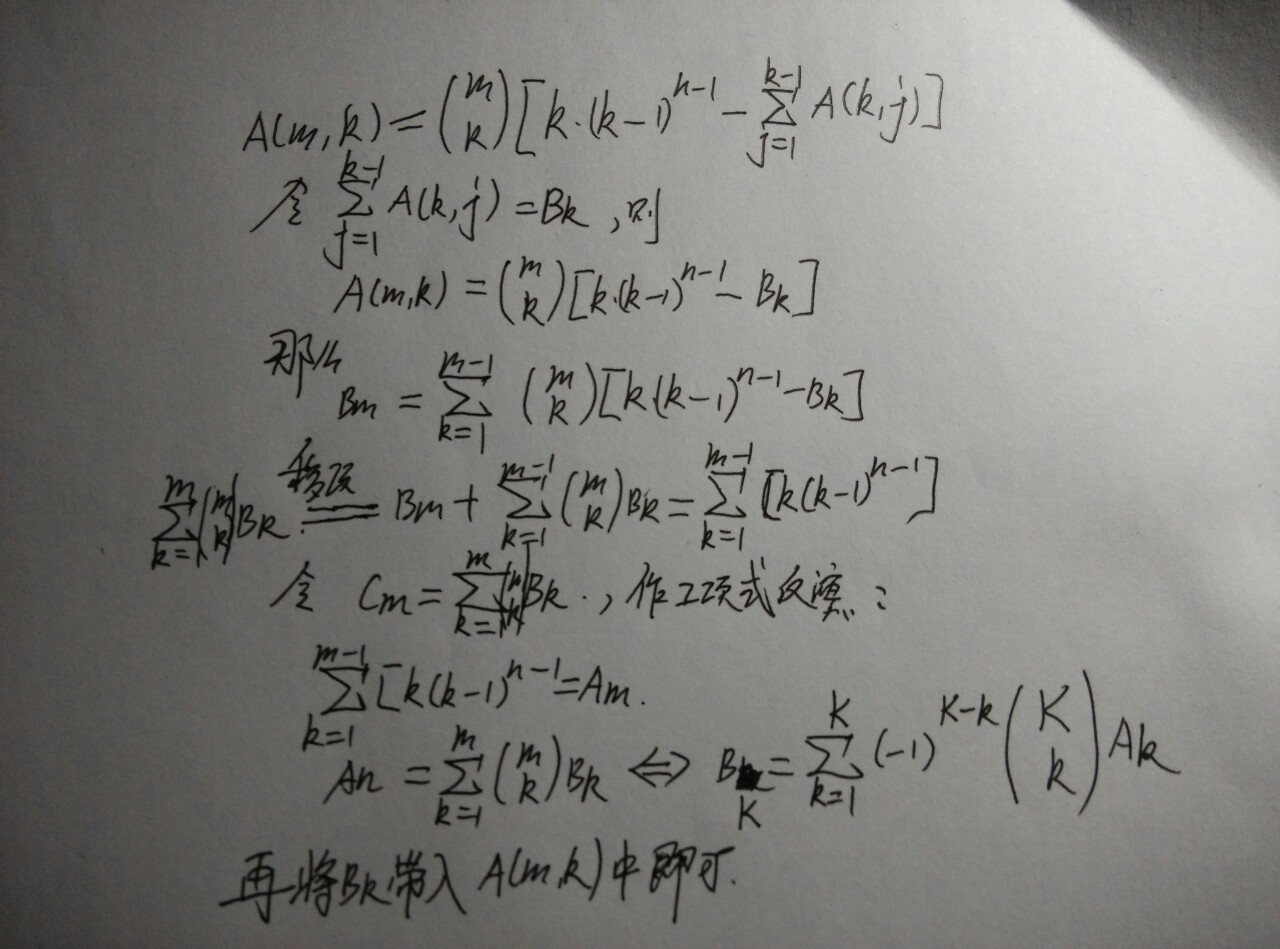
 期望时间O(K²)，还是不行。

3）在群里问，并且验证过的，最终的解法是：

F[k] = C(m, k) * k * (k-1)^n-1-F[k-1]

ans = F[k]

期望时间O(K)，这个需要证明

。。然后我证不出来，然后然后就没有然后了。。

#include <cstdio>
#include <cstring>
using namespace std;

typedef long long LL;
const int mod = 1e9+7;

int pow_mod(int p, int k)
{
    LL ans = 1;    
    while(k) {
        if (k & 1) ans = ans * p % mod;
        p = (LL)p*p % mod;
        k >>= 1;
    }
    return ans;
}

//以下为求逆元
///*************//
LL extend_gcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    LL gcd=extend_gcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-a/b*x;
    return gcd;
}
LL Get_Inverse(LL num)
{
    LL x,y;
    extend_gcd(num,mod,x,y);
    return (x%mod+mod)%mod;
}
///*************//
LL comb(LL n,LL m)//计算组合数C(n,m)
{
    LL t1=1,t2=1;
    for(LL i=n;i>m;i--)
    {
        t1=(t1*i)%mod;
        t2=(t2*(i-m))%mod;
    }
    return t1*Get_Inverse(t2)%mod;
}


/* 
int dp[10007][10007];

LL dfs(int N, int m, int k) {
    if (~dp[m][k]) return dp[m][k];
    LL ans = 0;
    for(int j = 1; j<k; ++j)
        ans = (ans + dfs(N, k,j)) % mod;
    return dp[m][k] = (comb(m, k)*(((LL)k*pow_mod(k-1, N-1) % mod - ans) % mod)) % mod;
}*/ 

int k_kdec[100007];

int main(void)
{
    int T;
    scanf("%d", &T);

    for(int t=1; t<=T; ++t) {
        int N, M, K;
        scanf("%d%d%d", &N, &M, &K);
        // memset(dp, -1, sizeof dp);
        // 暴力
        // printf("%d
", dfs(N, M, K));
        /*
        for(int m=1; m<=K; ++m) {
            k_kdec[m] = 0;
            for(int k=1; k<m; ++k)
                k_kdec[m] = (k_kdec[m] + (comb(m, k) * ((LL)k*pow_mod(k-1, N-1) % mod)) % mod) % mod;
        }
        // 二项式反演
        int sgn[] = {1, -1};
        int bk = 0;
        for(int k = 1; k<=K; ++k)
            bk = (bk +(sgn[(K-k) & 1] * (comb(K, k) * k_kdec[k]) % mod)) % mod;
        printf("%I64d
", (comb(M, K) * (((LL)K*pow_mod(K-1, N-1) % mod) - bk) % mod) % mod);*/
        
        // 容斥直接搞 
        LL ans = 0;
        int sgn = 1;
        for(int k = K; k>=1; --k) {
            ans = (ans + sgn * ((comb(M, k) * ((LL)k*pow_mod(k-1, N-1) % mod)) % mod)) % mod;
            sgn = -sgn;
        }
        printf("Case #%d: %d
", t, (int)ans);
    }
}